练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在△ABC中,a=,b=,B=45°,解此三角形.

    思路点拨:根据已知条件,此题是已知两边和一边的对角的题目,要根据条件先求出A,然后根据A的值,再讨论解的情况.

    解:由得sinA=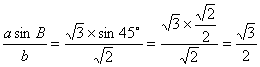.∵a＞b,∴A＞B=45°.∴A为锐角或钝角.∴A=60°或A=120°.当A=60°时,C=180°-60°-45°=75°,c=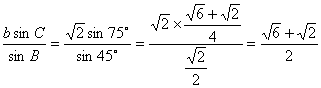.当A=120°时,C=180°-120°-45°=15°,c=.

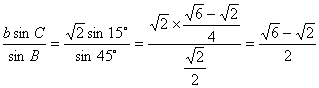    [一通百通]在给定条件解三角形时,要分清是可解的哪一类型,然后再根据不同类型的步骤去进行求解.特别注意的是已知两边与一边的对角,要根据情况进行讨论,有时有两解,有时有一解,有时无解.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知在△ABC中A=45°，AC=4
    		2
    ．若△ABC的解有且仅有一个，则BC满足的充要条件是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中∠A=60°，b=1，其面积为
    		3
    ，则角A的对边的长为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中a=4
    		6
     ，B=60°，C=75°    ，则b=
    12
    12
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    命题p：不等式|
    x
    x-1
    | ＞
    x
    x-1
    的解集为（0，1）；命题q：在△ABC中“A＞B”是“sinA＞sinB”成立的必要不充分条件，则（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中a，b，c分别为三内角A，B，C所对的边，若b=3，c=3
    		3
    ，A=30°    ，则角C等于（　　）

    查看答案和解析>>

    同步练习册答案