

(1)求cos〈![]() ,
,![]() 〉;
〉;
(2)求直线AD与平面ANM所成角的大小;
(3)求平面ANM与平面ABCD所成角的大小.
解:(1)如图,建立空间直角坐标系,则A(0,0,0),M(5,2,4),A1(0,0,4),D(0,8,0).

因为![]() =(5,2,4),
=(5,2,4),![]() =(0,8,-4),
=(0,8,-4),
所以![]() ·
·![]() =0+16-16=0.所以
=0+16-16=0.所以![]() ⊥
⊥![]() .
.
所以cos〈![]() ,
,![]() 〉=0.
〉=0.
(2)A1D⊥AM,A1D⊥AN,所以![]() ⊥平面AMN.
⊥平面AMN.
所以![]() =(0,8,-4)是平面ANM的一个法向量.
=(0,8,-4)是平面ANM的一个法向量.
又![]() =(0,8,0),|
=(0,8,0),|![]() |=4
|=4![]() ,|
,|![]() |=8,
|=8,![]() ·
·![]() =64,
=64,
所以cos〈![]() ,
,![]() 〉=
〉=![]() .
.
所以AD与平面AMN所成角为![]() -arccos
-arccos![]() .
.
(3)因为平面ANM的法向量是![]() =(0,8,-4),
=(0,8,-4),
平面ABCD的法向量是a=(0,0,1),
所以cos〈![]() ,a〉=
,a〉=![]() .
.
所以平面ANM与平面ABCD所成角的大小为arccos![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:044
如下图所示,在长方体
 中,
中, ,AB=2,点E在棱AB上移动.
,AB=2,点E在棱AB上移动.
(1)
证明: ;
;
(2)
当E为AB的中点时,求点E到面 的距离;
的距离;
(3)AE
等于何值时,二面角 的大小为
的大小为 .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
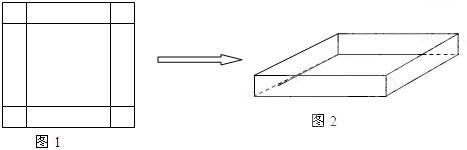
(本小题满分15分)在一次数学实践活动课上,老师给一个活动小组安排了这样的一个任务:设计一个方案,将一块边长为4米的正方形铁片,通过裁剪、拼接的方式,将它焊接成容积至少有5立方米的长方体无盖容器(只有一个下底面和侧面的长方体).该活动小组接到任务后,立刻设计了一个方案,如下图所示,按图1在正方形铁片的四角裁去四个相同的小正方形后,将剩下的部分焊接成长方体(如图2).请你分析一下他们的设计方案切去边长为多大的小正方形后能得到的最大容积,最大容积是多少?是否符合要求?若不符合,请你帮他们再设计一个能符合要求的方案,简单说明操作过程和理由. W ww.k s 5u.c om
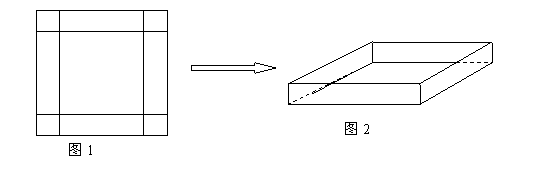

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com