

图19
探究:利用体积关系得到面积的关系解决此类问题,且灵活应用“转化”这一重要数学思想.截面A1EFD1为一个矩形,求其面积只要求出A1E的长度.注意到被两平行平面分割而成的三部分都是棱柱,其体积比也就是在侧面A1B被分割成的三个图形的面积比,于是容易得到各线段长度比进而得到线段AE的长度,再利用勾股定理容易得到A1E的长度.
解:因为V1∶V2∶V3=1∶4∶1,又棱柱AEA1—DFD1,EBE![]() ∶
∶![]() ∶
∶![]() =1∶4∶1.
=1∶4∶1.
所以![]() =
=![]() ×3×6=3,即
×3×6=3,即![]() ×3×AE=3.所以AE=2.
×3×AE=3.所以AE=2.
在Rt△A1AE中,A1E=![]() =
=![]() ,
,
所以截面A1EFD1的面积为A1E×A1D1=A1E×AD=4![]() .
.
答:截面A1EFD1的面积为4![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
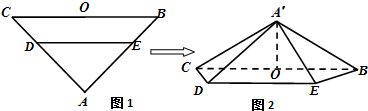 如图1,在等腰△ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,CD=BE=
如图1,在等腰△ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,CD=BE=| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
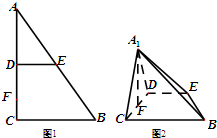 如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.
如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•北京)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.
(2012•北京)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:
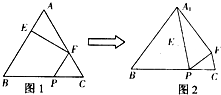 (2012•茂名一模)如图1,在正三角形ABC中,AB=3,E、F、P分别是AB、AC、BC边上的点,AE=CF=CP=1.将△AFE沿折起到△A1EF的位置,使平面A1EF与平面BCFE垂直,连接A1B、A1P(如图2).
(2012•茂名一模)如图1,在正三角形ABC中,AB=3,E、F、P分别是AB、AC、BC边上的点,AE=CF=CP=1.将△AFE沿折起到△A1EF的位置,使平面A1EF与平面BCFE垂直,连接A1B、A1P(如图2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com