
| 4 | x-3 |
科目:高中数学 来源:安徽省安庆市2007届高三数学调研测试卷 题型:022
规定记号“![]() ”表示两个正数间的一种运算:a
”表示两个正数间的一种运算:a![]() b=
b=![]() +a+b(a>0,b>0)
+a+b(a>0,b>0)
若1![]() k=3,则函数f(x)=k
k=3,则函数f(x)=k![]() x的值域是________.
x的值域是________.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省丹东市宽甸二中高三(上)期末数学试卷(解析版) 题型:选择题
 ;
;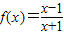 ,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集.
,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集.查看答案和解析>>
科目:高中数学 来源:四川省月考题 题型:填空题
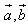 的夹角为锐角”的充要条件是“
的夹角为锐角”的充要条件是“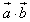 >0”;
>0”;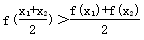 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com