
某连锁分店销售某种商品,每件商品的成本为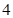 元,并且每件商品需向总店交
元,并且每件商品需向总店交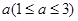 元的管理费,预计当每件商品的售价为
元的管理费,预计当每件商品的售价为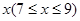 元时,一年的销售量为
元时,一年的销售量为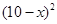 万件.
万件.
(Ⅰ)求该连锁分店一年的利润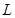 (万元)与每件商品的售价
(万元)与每件商品的售价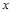 的函数关系式
的函数关系式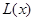 ;
;
(Ⅱ)当每件商品的售价为多少元时,该连锁分店一年的利润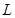 最大,并求出
最大,并求出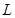 的最大值.
的最大值.
(Ⅰ)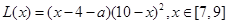 ;(Ⅱ)
;(Ⅱ)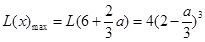 .
.
【解析】
试题分析:(Ⅰ)由题得该连锁分店一年的利润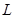 (万元)与售价
(万元)与售价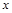 的函数关系式为
的函数关系式为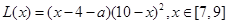 . (Ⅱ)要求
. (Ⅱ)要求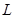 的最大值,需要利用导数求解,
的最大值,需要利用导数求解,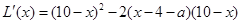
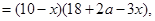 令
令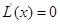 ,得
,得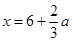 或
或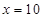 ,此函数中有参数
,此函数中有参数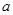 ,则需要对
,则需要对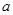 进行讨论,
进行讨论,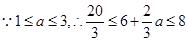 .①当
.①当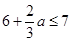 ,即
,即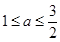 时,
时,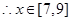 时,
时,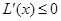 ,
,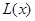 在
在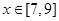 上单调递减,故
上单调递减,故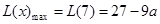 ;
②当
;
②当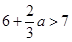 ,即
,即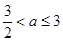 时,
时,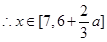 时,
时,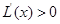 ;
;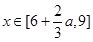 时,
时,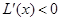
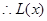 在
在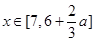 上单调递增;在
上单调递增;在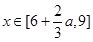 上单调递减,故
上单调递减,故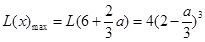 ,最后需要答.
,最后需要答.
试题解析:(Ⅰ)由题得该连锁分店一年的利润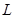 (万元)与售价
(万元)与售价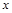 的函数关系式为
的函数关系式为
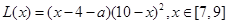 .
.
(Ⅱ)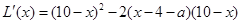
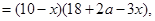
令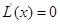 ,得
,得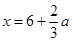 或
或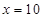
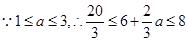 .
.
①当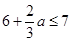 ,即
,即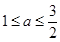 时,
时,
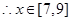 时,
时,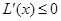 ,
,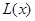 在
在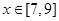 上单调递减,
上单调递减,
故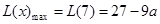
②当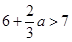 ,即
,即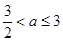 时,
时,
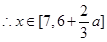 时,
时,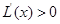 ;
;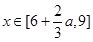 时,
时,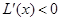
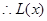 在
在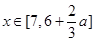 上单调递增;在
上单调递增;在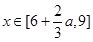 上单调递减,
上单调递减,
故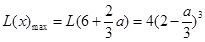
答:当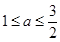 每件商品的售价为7元时,该连锁分店一年的利润
每件商品的售价为7元时,该连锁分店一年的利润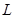 最大,最大值为
最大,最大值为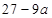 万元;
万元;
当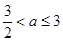 每件商品的售价为
每件商品的售价为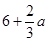 元时,该连锁分店一年的利润
元时,该连锁分店一年的利润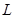 最大,最大值为
最大,最大值为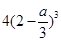 万元.
万元.
考点:1.根据题意列函数表达式;2.利用导数求函数最值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:《第1章 导数及其应用》2010年单元测试卷(2)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2007年福建省高考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011年高考数学复习:2.12 导数在研究函数中的应用与生活中的优化问题举例(1)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com