在平面直角坐标系xOy中,点P是第一象限内曲线y=-x3+1上的一个动点,点P处的切线与两个坐标轴交于A,B两点,则△AOB的面积的最小值为 .
【答案】
分析:根据题意设出点P的坐标,求出曲线方程的导函数,把点P的横坐标代入导函数求出的导函数值即为切线的斜率,根据切点和斜率表示出切线的方程,分别令x=0和y=0求出切线与两坐标轴的交点坐标,由交点坐标表示出△AOB的面积S,利用基本不等式即可求出面积的最小值时P横坐标的值,把此时P横坐标的值代入S中即可求出S的最小值.
解答:解:根据题意设P的坐标为(t,-t
3+1),且0<t<1,
求导得:y′=-3x
2,故切线的斜率k=y′
|x=t=-3t
2,
所以切线方程为:y-(-t
3+1)=-3t
2(x-t),
令x=0,解得:y=2t
3+1;令y=0,解得:x=
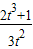
,
所以△AOB的面积S=

(2t
3+1)•
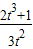
=

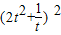
,
设y=2t
2+

=2t
2+
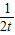
+
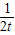
≥3
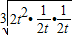
,
当且仅当2t
2=
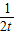
,即t
3=

,即t=
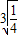
取等号,
把t=
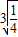
代入得:S
min=
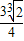
.
故答案为:
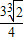 点评:
点评:解本题的思路是设出切点P的坐标,求出曲线方程的导函数,把P的横坐标代入导函数中求出切线的斜率,由切点坐标和斜率写出切线方程,求出切线与两坐标轴的交点坐标,进而表示出三角形ABC的面积S,变形后利用基本不等式即可求出S最小时P横坐标的值,把此时P的横坐标代入S即可求出S的最小值.要求学生掌握求导法则以及会利用基本不等式求函数的最小值.

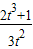 ,
, (2t3+1)•
(2t3+1)•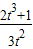 =
=
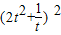 ,
, =2t2+
=2t2+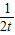 +
+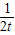 ≥3
≥3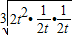 ,
,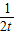 ,即t3=
,即t3= ,即t=
,即t=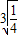 取等号,
取等号,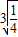 代入得:Smin=
代入得:Smin=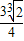 .
.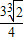


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是