分析:(I)在三棱柱ABC-A
1B
1C
1中,CC
1⊥平面ABC,利用线面垂直的性质定理可得 CC
1⊥BC.由已知 AC=BC=2,
AB=2,可得AC
2+BC
2=AB
2,利用勾股定理的逆定理得到BC⊥AC. 再利用线面垂直的判定定理可得BC⊥平面ACC
1A
1.进而利用线面垂直的性质定理即可得出结论.
(II) 过N作NP∥BB
1交AB
1于P,连接MP,则NP∥CC
1. 由已知 M,N分别为CC
1,AB中点,利用平行线分线段成比例定理可得
CM=CC1,
NP=BB1.进而可得四边形MCNP是平行四边形,利用其性质可得 CN∥MP.再利用线面平行的判定定理即可证明结论.
解答:证明:(Ⅰ)∵三棱柱ABC-A
1B
1C
1中CC
1⊥平面ABC,
∴CC
1⊥BC.
∵AC=BC=2,
AB=2,
∴AC
2+BC
2=AB
2,
∴BC⊥AC.
又∵AC∩CC
1=C,
∴BC⊥平面ACC
1A
1.
∵AM?平面ACC
1A
1,
∴BC⊥AM.
(Ⅱ)过N作NP∥BB
1交AB
1于P,连接MP,则NP∥CC
1.
∵M,N分别为CC
1,AB中点,
∴
CM=CC1,
NP=BB1.
∵BB
1=CC
1,
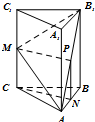
∴NP=CM.
∴四边形MCNP是平行四边形.
∴CN∥MP.
∵CN?平面AB
1M,MP?平面AB
1M,
∴CN∥平面AB
1 M.
点评:本题综合考查了线面垂直与平行的判定定理和性质定理、平行线分线段成比例定理、平行四边形的判定与性质定理、勾股定理的逆定理等基础知识与基本技能,考查了空间想象能力、推理能力和计算能力.

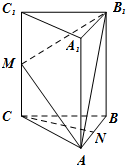 (2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2
(2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案