练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，是一块矩形铁板，剪掉四个阴影部分的小正方形，沿虚线折叠后，焊接成一个无盖的长方体水箱．

    (Ⅰ)写出水箱的容积与水箱高度的函数表达式，并求其定义域；

    (Ⅱ)当水箱高度为何值时，水箱的容积最大，并求出其最大值．

    解：(Ⅰ)由题意得

    ．

          (Ⅱ) ∵，

    ∴，

    令，即，

    解得，或（舍）．

    当变化时,的变化情况如下表：

    +

    最大值

    由上表可知，当时，容积有最大值，且最大值为立方厘米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

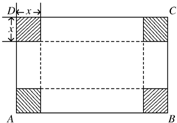    精英家教网如图，ABCD是一块矩形铁板AB=48cm，BC=30cm，剪掉四个阴影部分的小正方形，沿虚线折叠后，焊接成一个无盖的长方体水箱．
    （Ⅰ）写出水箱的容积V与水箱高度x的函数表达式，并求其定义域；
    （Ⅱ）当水箱高度x为何值时，水箱的容积V最大，并求出其最大值．

    查看答案和解析>>

    科目：高中数学 来源：教材完全解读　高中数学　必修5(人教B版课标版) 人教B版课标版 题型：044

    要想在一块圆心角为，半径为R的扇形铁板中截取一块矩形铁板，有如下两种方法：方法一是矩形的一边在半径上(如图甲)；方法二是矩形的两个顶点分别在两条半径上，另两个顶点在圆弧上(如图乙，其中OA＝OD)．

    试问：两种方法哪种截取的矩形面积大？并求出这个矩形的面积．

    查看答案和解析>>

    同步练习册答案