练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (理)如图，A(－1，0)，B(1，0)，曲线C1：y＝x2－1(|x|≥1)上一点M处的切线l与曲线C2：y＝－(|x|＜1)也相切于点N，记点M的横坐标为t(t＞1)．

    (Ⅰ)用t表示m的值和点N的坐标；

    (Ⅱ)当实数m取何值时，∠MAB＝∠NAB，并求此时MN所在直线的方程．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

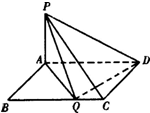    精英家教网（理）如图，矩形ABCD，|AB|=1，|BC|=a，PA⊥面ABCD且|PA|=1
    （1）BC边上是否存在点Q，使得FQ⊥QD，并说明理由；
    （2）若BC边上存在唯一的点Q使得FQ⊥QD，指出点Q的位置，并求出此时AD与平面PDQ所成的角的正弦值；
    （3）在（2）的条件下，求二面角Q-PD-A的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2004•宁波模拟）（理）如图，在矩形ABCD中，AB=3
    		3
    ，BC=3，沿对角线BD将△BCD折起，使点C移到点C'，且C'在平面ABD的射影O恰好在AB上．
    （1）求证：BC'⊥面ADC'；
    （2）求二面角A-BC'-D的大小；
    （3）求直线AB和平面BC'D所成的角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•崇明县二模）（理）如图，PA⊥平面ABCD，四边形ABCD是正方形，PA=AD=2，点E、F、G分别为线段PA、PD和CD的中点．
    （1）求异面直线EG与BD所成角的大小；
    （2）在线段CD上是否存在一点Q，使得点A到平面EFQ的距离恰为
    45
    ？若存在，求出线段CQ的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

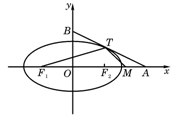
    （06年浙江卷理）（14分）

    如图，椭圆＝1（a＞b＞0）与过点A（2，0）B(0,1)的直线有且只有一个公共点T，且椭圆的离心率e=.

     (Ⅰ)求椭圆方程；

    (Ⅱ)设F、F分别为椭圆的左、右焦点，M为线段AF的中点，求证：∠ATM=∠AFT.

    查看答案和解析>>

    同步练习册答案