Question

已知函数f(x)＝lg |x|.

(1)判断函数f(x)的奇偶性；

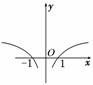
(2)画出函数f(x)的草图；

(3)求函数f(x)的单调递减区间，并加以证明．

Answer 1

解：(1)要使函数有意义，x的取值需满足|x|>0，

解得x≠0，即函数的定义域是

(－∞，0)∪(0，＋∞)，

f(－x)＝lg |－x|＝lg |x|＝f(x)，

∴f(－x)＝f(x)．

∴函数f(x)是偶函数．

(2)由于函数f(x)是偶函数，则其图象关于y轴对称，如图所示．

(3)由图得函数f(x)的单调递减区间是(－∞，0)．

证明：设x₁、x₂∈(－∞，0)，且x₁<x₂，

则f(x₁)－f(x₂)＝lg |x₁|－lg |x₂|＝lg .

∵x₁、x₂∈(－∞，0)，且x₁<x₂，

∴|x₁|>|x₂|>0.

∴>1.

∴lg >0.

∴f(x₁)>f(x₂)．

∴函数f(x)在(－∞，0)上是减函数，

即函数的单调递减区间是(－∞，0)．