已知：
＝(
sinx，cosx)，
＝(cosx，cosx)，f(x)＝2·＋2m－1(x，m∈R)．
(Ⅰ)求f(x)关于x的表达式，并求f(x)的最小正周期；
(Ⅱ)若x∈[0，
]时，f(x)的最小值为5，求m的值．
寒假天地重庆出版社系列答案科目：高中数学 来源：山西省山大附中2011－2012学年高一下学期期中考试数学试题 题型：044
已知向量
＝(sinx，－1)，
＝(
cosx，－
)，函数f(x)＝(＋)·－2
(1)求函数f(x)的最小正周期T；
(2)将函数f(x)的图像向左平移
上个单位后，再将所得图像上所有点的横坐标伸长为原来的3倍，得到函数g(x)的图像，求函数g(x)的解析式及其对称中心坐标
查看答案和解析>>
科目：高中数学 来源：四川眉山市高中2007届第二次诊断考试、数学(理科) 题型：038
已知向量
＝(sinx，2
cosx)，
＝(2sinx，sinx)，设f(x)＝·－1
①若x
[0，
]，求f(x)的值域．
②若f(x)的图象可以按向量
平移后得到y＝2cos2x的图象，指出向量的一个值．
查看答案和解析>>
科目：高中数学 来源：黑龙江省大庆铁人中学2012届高三上学期期中考试数学理科试题 题型：044
已知向量
＝(sinx，－1)，向量
＝(
cosx，－
，函数f(x)＝(＋)·．
(Ⅰ)求f(x)的最小正周期T；
(Ⅱ)已知a，b，c分别为△ABC内角A，B，C的对边，A为锐角，a＝2
，c＝4，且f(A)恰是f(x)在[0，
]上的最大值，求A，b和△ABC的面积S．
查看答案和解析>>
科目：高中数学 来源：2014届河北省高一12月月考数学试卷 题型：解答题
已知a＝(sinx，－cosx)，b＝(cosx，
cosx)，函数 f(x)＝a.·b＋
.
(1)求 f(x)的最小正周期，并求其图象对称中心的坐标；
(2)当0≤x≤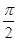
时，求函数 f(x)的值域．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
