练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设|z|＝1，且z2＋2z＋＜0，求复数z．

    答案：
    解析：

    　　解：|z|＝1，∴z＝1，∴．设z＝a＋bi(a，b∈R)，∴a2＋b2＝1．

    　　∴z2＋2z＋＝z2＋2z＋＝(a2－b2)＋2abi＋2a＋2bi＋a－bi＝(a2－b2＋3a)＋(2ab＋b)i＜0．

    　　∴

    　　∴z＝－1或

    　　分析：本题考查模的性质、复数的代数运算等知识．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：“伴你学”新课程　数学·选修1－2(人教B版) 人教B版 题型：013

    设z1＝4＋3，z2＝－1＋2i且f(z)＝，则是

    [　　]
    A．

    3＋5i

    B．

    5＋i

    C．

    5－i

    D．

    3－i

    查看答案和解析>>

    科目：高中数学 来源：设计选修数学－1-2苏教版 苏教版 题型：044

    设|Z|＝1，且Z2＋2Z＋＜0，求复数Z．

    查看答案和解析>>

    科目：高中数学 来源：云南省玉溪一中2011－2012学年高一下学期期末考试数学试题 题型：044

    (1)设x、y、z1∈R，且x＋y＋z＝1，求证x2＋y2＋z2≥；

    (2)设二次函数f(x)＝ax2＋bx＋c(a＞0)，方程f (x)－x＝0有两个实根x1，x2，且满足：0＜x1＜x2＜，若x∈(0，x1)．

    求证：x＜f(x)＜x1

    查看答案和解析>>

    科目：高中数学 来源：2014届云南省高一下学期期末数学试卷（解析版） 题型：解答题

    （12分）（1）设x、y、zR，且x＋y＋z＝1，求证x2＋y2＋z2≥；

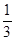    （2）设二次函数f (x)＝ax2＋bx＋c （a＞0），方程f (x)－x＝0有两个实根x1，x2，

    且满足：0＜x1＜x2＜，若x(0，x1)。

    求证：x＜f (x)＜x1

     

    查看答案和解析>>

    同步练习册答案