练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数f(x)=x+tan2x(x∈R,且x≠kπ+,k∈Z)使(    )

    A.f(-x)=-f(x)成立                              B.f(-x)=f(x)成立

    C.f(-x)=±f(x)都成立                         D.f(-x)=±f(x)都不成立

    解析:∵f(-x)=tan(-2x)-x=-tan2x-x=-(tan2x+x)=-f(x),

    ∴函数f(x)=tan2x+x使f(-x)=-f(x)成立.

    答案:A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：数学教研室 题型：013

    下列说法正确的是

    [　　]

    A．对于函数f(x)，如果存在一个常数T，使得定义域内的每一个x值都满足f(x＋T)=f(x)，则函数f(x)叫做周期函数

    B．对于函数f(x)，如果存在一个非零常数T，使得定义域内存在一个x满足于f(x＋T)=f(x)，则f(x)叫做周期函数

    C．对于函数f(x)，如果存在一个非零常数T，使得定义域内存在若干个x满足f(x＋T)=f(x)，则f(x)叫做周期函数

    D．对于函数f(x)，如果存在一个非零常数T，使得定义域的每一个x值满足f(x＋T)=f(x)，则f(x)叫做周期函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

    下列说法正确的是

    [　　]

    A．对于函数f(x)，如果存在一个常数T，使得定义域内的每一个x值都满足f(x＋T)=f(x)，则函数f(x)叫做周期函数

    B．对于函数f(x)，如果存在一个非零常数T，使得定义域内存在一个x满足于f(x＋T)=f(x)，则f(x)叫做周期函数

    C．对于函数f(x)，如果存在一个非零常数T，使得定义域内存在若干个x满足f(x＋T)=f(x)，则f(x)叫做周期函数

    D．对于函数f(x)，如果存在一个非零常数T，使得定义域的每一个x值满足f(x＋T)=f(x)，则f(x)叫做周期函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π，x∈R）的导函数f′（x）的图象上的一个最高点和与它相邻的一个最低点的坐标分别为M（-数学公式，3），N（数学公式，-3）．
    （Ⅰ）求函数f（x）的解析式；
    （Ⅱ）将函数f（x）的图象向右平移数学公式个单位得到函数g（x）图象，直线x=t（t∈[0，数学公式]）与f（x），g（x）的图象分别交于P，Q两点，求|PQ|的最大值．

    查看答案和解析>>

    科目：高中数学 来源：2010年山东省威海市高考模拟数学试卷（理科）（解析版） 题型：解答题

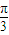    已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π，x∈R）的导函数f′（x）的图象上的一个最高点和与它相邻的一个最低点的坐标分别为M（-，3），N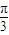（，-3）．
    （Ⅰ）求函数f（x）的解析式；
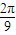    （Ⅱ）将函数f（x）的图象向右平移个单位得到函数g（x）图象，直线x=t（t∈[0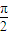，]）与f（x），g（x）的图象分别交于P，Q两点，求|PQ|的最大值．

    查看答案和解析>>

    科目：高中数学 来源：2010年山东省威海市高考模拟数学试卷（文科）（解析版） 题型：解答题

    已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π，x∈R）的导函数f′（x）的图象上的一个最高点和与它相邻的一个最低点的坐标分别为M（-，3），N（，-3）．
    （Ⅰ）求函数f（x）的解析式；
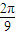    （Ⅱ）将函数f（x）的图象向右平移个单位得到函数g（x）图象，直线x=t（t∈[0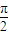，]）与f（x），g（x）的图象分别交于P，Q两点，求|PQ|的最大值．

    查看答案和解析>>

    同步练习册答案