
思路分析:解题目标——找出θ1、θ2与α、β的联系,不妨利用a·b=|a||b|cosθ试试?
解:∵α∈(0,π),β∈(π,2π),
∴|a|=![]() =2|cos
=2|cos![]() |=2cos
|=2cos![]() ,
,
|b|=![]() =2|sin
=2|sin![]() |=2sin
|=2sin![]() ,
,
|c|=1,a·c=1+cosα=2cos2![]() ,b·c=1-cosβ=2sin2
,b·c=1-cosβ=2sin2![]() ,
,
∴cosθ1=![]() .
.
∵θ1∈[0,π],![]() ∈(0,
∈(0,![]() )
)![]() [0,π],y=cosx的值在[0,π]上与x的值一一对应,∴θ1=
[0,π],y=cosx的值在[0,π]上与x的值一一对应,∴θ1=![]() .
.
cosθ2=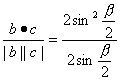
=sin![]() =cos(
=cos(![]() -
-![]() ),
),
∵θ2∈[0,π],![]() -
-![]() ∈(0,
∈(0,![]() )
)![]() (0,π),y=cosx的值在[0,π]上与x的值一一对应,
(0,π),y=cosx的值在[0,π]上与x的值一一对应,
∴θ2=![]() -
-![]() .又θ1-θ2=
.又θ1-θ2=![]() ,
,
∴![]() -
-![]() +
+![]() =
=![]() ,
,
∴![]() =-
=-![]() ,
,
∴sin![]() =sin(-
=sin(-![]() )=-
)=-![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| a |
| π |
| 2 |
| AB |
| a |
| AB |
| 5 |
| OA |
| OB |
| AC |
| a |
| OA |
| OC |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| AB |
| a |
| OB |
| AC |
| a |
| OA |
| OC |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| b |
| c |
| π |
| 3 |
| a |
| c |
| a |
| c |
| b |
| c |
| a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com