
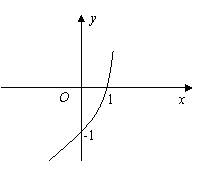
 已知函数
已知函数![]() 的图像如图所示,数列
的图像如图所示,数列![]() 的前
的前![]() 项的和
项的和![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项的和,且
项的和,且![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)找出所有满足:![]() 的自然数
的自然数![]() 的值(不必证明);
的值(不必证明);
(3)若不等式![]() 对于任意的
对于任意的![]() ,
,![]() 恒成立,
恒成立,
求实数![]() 的最小值,并求出此时相应的
的最小值,并求出此时相应的![]() 的值.
的值.
解:(1)由题意得:![]() ,解之得:
,解之得:![]() ,
,![]()
![]() 当
当![]() 时,
时,![]()
当![]() 时,
时,![]() 符合上式,故
符合上式,故![]() ,
,![]() . -----------------------------2分
. -----------------------------2分
当![]() 时,
时,![]()
当![]() 时,
时,![]() 不符合上式,故
不符合上式,故![]() . -------------------------4分
. -------------------------4分
(2)当![]() 时,
时,![]() ,且
,且![]() ,不合
,不合
当![]() 时,由题意可得:
时,由题意可得:![]()
而方程![]() 只有
只有![]() 满足条件,故当
满足条件,故当![]() 时,
时,![]() -----------------------6分
-----------------------6分
(3)由题得:
![]() ,
,![]() 对于一切
对于一切![]() ,
,![]() 恒成立
恒成立
即![]() --------------------------8分
--------------------------8分
令![]() (
(![]() ,
,![]() )则
)则![]()
![]() ------------------------10分
------------------------10分
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
而![]() ,
,![]()
![]()
故当![]() 时,
时,![]() 的最小值为46. ----------------------------14分
的最小值为46. ----------------------------14分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013届山东冠县武训高中高二下学期模块考试理科数学试卷(解析版) 题型:选择题
已知函数 的图像如图所示,
的图像如图所示, 是
是 的导函数,则下列数值排序正确的是
的导函数,则下列数值排序正确的是
A. B.
B.
C. D.
D.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com