分析:(1)设AM与A1C交于H,证出AM⊥面BCA1,得出∠BHC为二面角B-AM-C的平面角,得出△BCH为等腰直角三角形,∠BHC=45°
(2)在ABC 中,作CD⊥AB于D,连接 DM,在△MCD中,作 CO⊥MD,则CO⊥面 MAB,CO为点C到平面ABM的距离,在△MDC中求CO即可.
解答:解:(1)
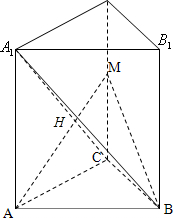
由直三棱柱得性质,侧面A
1C⊥底面ABC,BC⊥AC,BC⊥面A
1C,∴BC⊥AM,又AM⊥BA
1∴AM⊥面BCA
1,垂足为H,AH⊥CH.连接BH,BH?面BCA
1,∴AM⊥BH,∠BHC为二面角B-AM-C的平面角.在直角三角形A1AC中,A
1C=3,由直角三角形射影定理,得出CH=1,又CB=1,∴△BCH为等腰直角三角形,∠BHC=45°,二面角B-AM-C大小为45°.
(2)
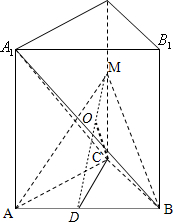
在ABC 中,作CD⊥AB于D,连接 DM,则 AB⊥面MCD,AB?面 MAB,∴面 MAB面⊥面 MCD 且交线为 MD,在△MCD中,作 CO⊥MD,则CO⊥面 MAB,CO为点C到平面ABM的距离.
由△CMO∽△A1AO,得出MC=
,又CD=
,由勾股定理得MD=
,利用等面积法:MD×CO=MC×CD,∴CO=
,即点C到平面ABM的距离是
.
点评:本题考查二面角的计算,空间距离的计算,线面垂直,面面垂直的定义,性质、判定,考查了空间想象能力、计算能力,分析解决问题能力.空间问题平面化是解决空间几何体问题最主要的思想方法.

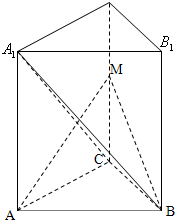 在直三棱柱ABC-A1B1C1中,∠ACB=90°,CB=1,CA=
在直三棱柱ABC-A1B1C1中,∠ACB=90°,CB=1,CA= 由直三棱柱得性质,侧面A1C⊥底面ABC,BC⊥AC,BC⊥面A1C,∴BC⊥AM,又AM⊥BA1
由直三棱柱得性质,侧面A1C⊥底面ABC,BC⊥AC,BC⊥面A1C,∴BC⊥AM,又AM⊥BA1 在ABC 中,作CD⊥AB于D,连接 DM,则 AB⊥面MCD,AB?面 MAB,∴面 MAB面⊥面 MCD 且交线为 MD,在△MCD中,作 CO⊥MD,则CO⊥面 MAB,CO为点C到平面ABM的距离.
在ABC 中,作CD⊥AB于D,连接 DM,则 AB⊥面MCD,AB?面 MAB,∴面 MAB面⊥面 MCD 且交线为 MD,在△MCD中,作 CO⊥MD,则CO⊥面 MAB,CO为点C到平面ABM的距离.

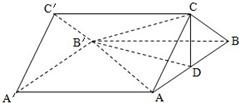 如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点.
如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点. 如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数).
如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数). 如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角.
如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角. 如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,
如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,