
(1)求证:CC1⊥BD;
(2)当![]() 的值为多少时,能使A1C⊥平面C1BD,并给出证明.
的值为多少时,能使A1C⊥平面C1BD,并给出证明.
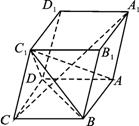
(1)证明:设![]() =a,
=a,![]() =b,
=b,![]() =c,∴
=c,∴![]() =c-b,∵∠C1CB=∠C1CD=∠BCD=60°,且底面ABCD为菱形,∴|b|=|c|,∴
=c-b,∵∠C1CB=∠C1CD=∠BCD=60°,且底面ABCD为菱形,∴|b|=|c|,∴![]() ·
·![]() =a·(c-b)=a·c-a·b=|a||c|cos60°-|a||b|cos 60°=0,
=a·(c-b)=a·c-a·b=|a||c|cos60°-|a||b|cos 60°=0,
∵![]() ⊥
⊥![]() ,∴CC1⊥BD.
,∴CC1⊥BD.
(2)证明:∵ABCD是菱形,∴BD⊥AC.
又∵BD⊥CC1.∴![]() ⊥平面A1C1CA.
⊥平面A1C1CA.
∴A1C![]() 平面A1C1CA.∴BD⊥A1C.
平面A1C1CA.∴BD⊥A1C.
∴要使A1C⊥平面C1BD,只要使A1C⊥BC1,即![]() ·
·![]() =0.
=0.
∵![]() =a+b+c,
=a+b+c,![]() =a-b,
=a-b,![]() ·
·![]() =(a+b+c)·(a-b)
=(a+b+c)·(a-b)
=|a|2+a·b+a·c-a·b-|b|2-b·c
=|a|2+|a||c|
cos 60°-|b|2-|b||c|cos 60°
=|a|2+![]() |a||c|-
|a||c|-![]() |c|2=0,
|c|2=0,
∴2|a|2+|a||c|-3|c|2=0.
∴(|a|+3|c|)(|a|-|c|)=0.
∴|a|=|c|,
即当![]() =1时,能使A1C⊥平面C1BD.
=1时,能使A1C⊥平面C1BD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且
如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且| OA |
| a |
| OC |
| b |
| OO1 |
| c |
| a |
| b |
| c |
| OG |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱)
如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱)查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com