解:(1)根据题意,令log
ax=t,则x=a
t,
所以

,即

当a>1时,因为a
x-a
-x为增函数,且

>0,所以f(x)在(-1,1)上为增函数;
当0<a<1时,因为a
x-a
-x为减函数,且

<0,所以f(x)在(-1,1)上为增函数;
综上所述,f(x)在(-1,1)上为增函数.
又因为f(-x)=
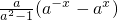
=-f(x),故f(x)为奇函数.
所以f(1-m)+f(1-m
2)<0?f(1-m)<-f(1-m
2)?f(1-m)<f(m
2-1)
由f(x)在(-1,1)上为增函数,可得
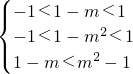
解得1<m<

,即m的值的集合为{m|1<m<

}
(2)由(1)可知,f(x)为增函数,
则要使x∈(-∞,2),f(x)-4的值恒为负数,
只要f(2)-4<0即可,即f(2)=

=

<4,又a>0
解得

又a≠1,可得符合条件的a的取值范围是(2-

,1)∪(1,2+

).
分析:(1)首先根据题意,用换元法求出f(x)的解析式,进而分析函数的单调性和奇偶性,将已知不等式转化为f(1-m)<f(m
2-1),进而转化为
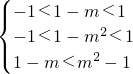
,解可得答案;
(2)由(1)中的单调性可将f(x-4)的值恒为负数转化为f(2)-4≤0,解不等式即可.
点评:本题考查函数奇偶性与单调性的综合运用,是综合题,解题时尤其注意正确求解不等式组的解集.

 (x-x-1),其中a>0,a≠1
(x-x-1),其中a>0,a≠1 ,即
,即
 >0,所以f(x)在(-1,1)上为增函数;
>0,所以f(x)在(-1,1)上为增函数; <0,所以f(x)在(-1,1)上为增函数;
<0,所以f(x)在(-1,1)上为增函数;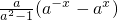 =-f(x),故f(x)为奇函数.
=-f(x),故f(x)为奇函数.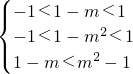
 ,即m的值的集合为{m|1<m<
,即m的值的集合为{m|1<m< }
} =
= <4,又a>0
<4,又a>0
 ,1)∪(1,2+
,1)∪(1,2+ ).
).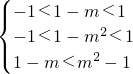 ,解可得答案;
,解可得答案;

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案