练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    数集与数集之间的关系是

    [　　]

    A．MN

    B．MÌ N

    C．M＝N

    D．M≠N
    答案：C
    解析：

    解法一：对M中任一元素(2n＋1)π，∵nÎZ，

    故n＝2k时，(2n＋1)π＝(4k＋1)πÎN，

    n＝2k－1时，(2n＋1)π＝(4k－1)πÎN．∴MÍ N．

    同理可证NÍM．故M＝N．

    解法二：∵被2除余1的整数的全体是奇数，被4除余1或3的整数的全体也是全体奇数，

    ∴2n＋1(nÎZ)和4k±1(kÎZ)都表示全体奇数，故M＝N．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（x）的定义域关于原点对称，且满足以下三个条件：
    ①x1、x2、x1-x2是定义域中的数时，有f(x1-x2)=
    f(x1)f(x2)+1f(x2)-f(x1)
    ；
    ②f（a）=-1（a＞0，a是定义域中的一个数）；
    ③当0＜x＜2a时，f（x）＜0．
    （1）判断f（x1-x2）与f（x2-x1）之间的关系，并推断函数f（x）的奇偶性；
    （2）判断函数f（x）在（0，2a）上的单调性，并证明；
    （3）当函数f（x）的定义域为（-4a，0）∪（0，4a）时，
     ①求f（2a）的值；②求不等式f（x-4）＜0的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

    下列命题

    ①互为共轭复数的两数之差必是纯虚数；

    ②如果让实数a与纯虚数ai对应，那么实数集与纯虚数集之间具有一一对应关系；

    ③复平面上，虚轴上的各点与纯虚数是一一对应的；

    ④在复平面上与复数3+4i对应的向量是唯一确定的.

    其中，正确命题的个数是　　　

    [　　]

    A.0个　　　B.1个　　　C.2个　　　D.3个

    查看答案和解析>>

    科目：高中数学 来源：湖北省黄冈中学2011－2012学年高一上学期期中考试数学试题 题型：044

    已知函数f(x)的定义域关于原点对称，且满足以下三个条件：

    ①x1、x2、x1－x2是定义域中的数时，有f(x1－x2)＝；

    ②f(a)＝－1(a＞0，a是定义域中的一个数)；

    ③当0＜x＜2a时，f(x)＜0．

    (1)判断f(x1－x2)与f(x2－x1)之间的关系，并推断函数f(x)的奇偶性；

    (2)判断函数f(x)在(0，2a)上的单调性，并证明；

    (3)当函数f(x)的定义域为(－4a，0)∪(0，4a)时，

    ①求f(2a)的值；

    ②求不等式f(x－4)＜0的解集．

    查看答案和解析>>

    科目：高中数学 来源：2015届河南省高一第一次阶段数学试卷（奥赛班）（解析版） 题型：解答题

    已知函数的定义域关于原点对称，且满足以下三个条件：

    ①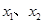、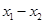是定义域中的数时，有；

    ②是定义域中的一个数）；

    ③当时，．

    （1）判断与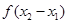之间的关系，并推断函数的奇偶性；

    （2）判断函数在上的单调性，并证明；

    （3）当函数的定义域为时，

    ①求的值；②求不等式的解集．

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年湖北省黄冈中学高一（上）期中数学试卷（解析版） 题型：解答题

    已知函数f（x）的定义域关于原点对称，且满足以下三个条件：
    ①x1、x2、x1-x2是定义域中的数时，有；
    ②f（a）=-1（a＞0，a是定义域中的一个数）；
    ③当0＜x＜2a时，f（x）＜0．
    （1）判断f（x1-x2）与f（x2-x1）之间的关系，并推断函数f（x）的奇偶性；
    （2）判断函数f（x）在（0，2a）上的单调性，并证明；
    （3）当函数f（x）的定义域为（-4a，0）∪（0，4a）时，
     ①求f（2a）的值；②求不等式f（x-4）＜0的解集．

    查看答案和解析>>

    同步练习册答案