
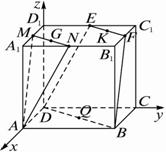
证明:建立如图坐标系,则A(4,0,0), M(2,0,4), N(4,2,4), D(0,0,0), B(4,4,0), E(0,2,4), F(2,4,4).
取MN的中点G及EF的中点K,BD的中点Q,则G(3,1,4),K(1,3,4),Q(2,2,0).
∴![]() =(2,2,0),
=(2,2,0), ![]() =(2,2,0),
=(2,2,0), ![]() =(-1,1,4),
=(-1,1,4), ![]() =(-1,1,4).
=(-1,1,4).
可见![]() =
=![]() ,
,![]() =
=![]() ,
,
∴MN∥EF,AG∥QK.
∴MN∥平面EFBD,AG∥平面EFBD.
∴平面AMN∥平面EFBD.?
温馨提示:(1)证面面平行,要证一个平面内的两条不共线的向量分别与另一个平面平行.(2)本题还可先求这两个平面的法向量,然后证明这两个法向量平行.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的:
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的:查看答案和解析>>
科目:高中数学 来源: 题型:
 已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点.
已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点.| GP |
| GH |
| ||
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积.
如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com