
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014届山东省高二下学期3月月考理科数学试卷(解析版) 题型:选择题
用数学归纳法证明(n+1)(n+2)(n+3)…(n+n)=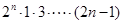 (n∈N*)时,从n=k到n=k+1,左端需要增加的代数式为( )
(n∈N*)时,从n=k到n=k+1,左端需要增加的代数式为( )
A.2k+1 B.2(2k+1) C.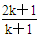 D.
D.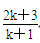
查看答案和解析>>
科目:高中数学 来源:2013届广东省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
用数学归纳法证明“(n+1)(n+2)·…·(n+n)=2n·1·3·…·(2n-1)”,从“k到k+1”左端需增乘的代数式为( )
A.2k+1 B.2(2k+1)
C. D..
D.. 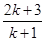
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com