练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数，不计算函数值，比较f(－1)、f(1)、f(4)、f(5)的大小．

    答案：略
    解析：

    ，

    对称轴为x=2，在区间[2，＋¥ )上为增函数．

    ∴f(－1)=f(2－3)=f(2＋3)=f(5)．

    f(1)=f(2－1)=f(2＋1)=f(3)．

    ∵函数f(x)在[2，＋¥ )上为增函数，

    ∴f(3)＜f(4)＜f(5)．

    故f(1)＜f(4)＜f(－1)=f(5)．


    提示：

    要认真领会这种转化的思想方法．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：设计必修一数学(人教A版) 人教A版 题型：044

    已知函数f(x)＝－x2－3x－．

    (1)求图象的开口方向、对称轴、顶点坐标、与x轴的交点坐标；

    (2)求函数的单调区间、最值和零点；

    (3)设图象与x轴相交于(x1，0)、(x2，0)，不求出根，求|x1－x2|；

    (4)已知f(－)＝，不计算函数值，求f(－)；

    (5)不计算函数值，试比较f(－)与f(－)的大小；

    (6)写出使函数值为负数的自变量x的集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

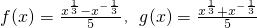    已知函数数学公式，分别计算f（4）-5f（2）g（2）和f（9）-5f（3）g（3）的值，并概括出涉及函数f（x）和g（x）的对所有不等于零的实数x都成立的一个等式：________．

    查看答案和解析>>

    科目：高中数学 来源：2009年上海市南汇区高考数学一模试卷（文科）（解析版） 题型：解答题

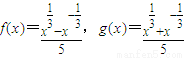    已知函数，分别计算f（4）-5f（2）g（2）和f（9）-5f（3）g（3）的值，并概括出涉及函数f（x）和g（x）的对所有不等于零的实数x都成立的一个等式：    ．

    查看答案和解析>>

    科目：高中数学 来源：2009年上海市南汇区高考数学一模试卷（理科）（解析版） 题型：解答题

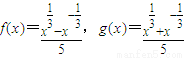    已知函数，分别计算f（4）-5f（2）g（2）和f（9）-5f（3）g（3）的值，并概括出涉及函数f（x）和g（x）的对所有不等于零的实数x都成立的一个等式：    ．

    查看答案和解析>>

    同步练习册答案