
如图,四棱锥![]() 中,
中, ![]() ∥
∥![]() ,
,![]() ,侧面
,侧面![]() 为等边三角形.
为等边三角形.![]()
![]() .
.
(I) 证明:![]()
(II) 求AB与平面SBC所成角的大小。
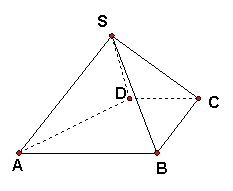
【思路点拨】第(I)问的证明的突破口是利用等边三角形SAB这个条件,找出AB的中点E,连结SE,DE,就做出了解决这个问题的关键辅助线。
(II)本题直接找线面角不易找出,要找到与AB平行的其它线进行转移求解。
【精讲精析】证明:(I)取AB中点E,连结DE,则四边形BCDE为矩形,DE=CB=2。
连结SE,则![]()
又SD=1,故![]()
所以![]() 为直角。
为直角。
由![]() ,得
,得
![]() ,所以
,所以![]() .
.
SD与两条相交直线AB、SE都垂直。
所以![]()
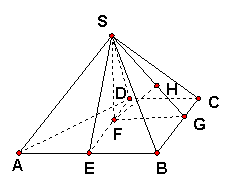
(II)由![]() 知,
知,![]()
作![]() ,垂足为F,则
,垂足为F,则![]() ,
,![]()
作![]() ,垂足为G,则FG=DC=1。
,垂足为G,则FG=DC=1。
连结SG,则![]()
又![]() ,
,![]() ,故
,故![]() ,
,
作![]() ,H为垂足,则
,H为垂足,则![]() .
.
![]()
即F到平面SBC的距离为![]() 。
。
由于ED//BC,所以ED//平面SBC,E到平面SBC的距离d也为![]() 。
。
设AB与平面SBC所成的角为![]() ,则
,则![]() ,
,![]() .
.
解法二:
以C为坐标原点,射线CD为x轴正半轴,建立如图所示的直角坐标系C-xyz,设D(1,0,0),则A(2,2,0),B(0,2,0)。
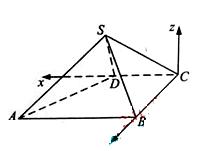
又设S(x,y,z),则x>0,y>0,z>0.
(I)![]()
由![]() 得
得
故x=1.
由![]() 得
得![]() ,
,
又由![]() 得,
得,![]()
即![]() ,故
,故![]() 。
。
于是![]() ,
,
![]()
故![]() ,又
,又![]()
所以![]() .
.
(II)设平面SBC的法向量![]() ,
,
则![]()
又![]()
故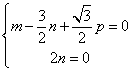
取![]() 得
得![]() ,又
,又![]()
![]() .
.
故AB与平面SBC所成的角为![]() .
.


科目:高中数学 来源: 题型:
 如图,四棱锥中,底面ABCD是菱形,SA=SD=
如图,四棱锥中,底面ABCD是菱形,SA=SD=| 39 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•聊城一模)如图,四棱锥中S-ABCD中,底面ABCD是棱形,其对角线的交点为O,且SA=AC,SA⊥BD,
(2011•聊城一模)如图,四棱锥中S-ABCD中,底面ABCD是棱形,其对角线的交点为O,且SA=AC,SA⊥BD,查看答案和解析>>
科目:高中数学 来源:2011届河北省邯郸一中高三高考压轴模拟考试文数 题型:解答题
(本小题12分)如图,四棱锥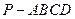 中,
中,
侧面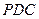 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面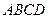 是
是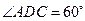 的菱形,
的菱形,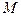 为
为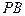 的中点.
的中点.
(1)求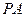 与底面
与底面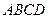 所成角的大小;
所成角的大小;
(2)求证: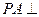 平面
平面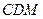 ;
;
(3)求二面角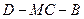 的余弦值.
的余弦值. 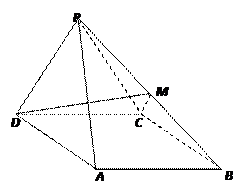
查看答案和解析>>
科目:高中数学 来源:2014届安徽省高三上学期第一次联考理科数学试卷(解析版) 题型:解答题
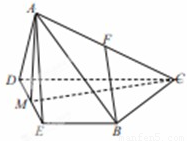
如图,四棱锥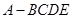 中,侧面
中,侧面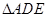 是等边三角形,在底面等腰梯形
是等边三角形,在底面等腰梯形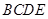 中,
中,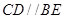 ,
,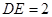 ,
,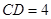 ,
,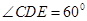 ,
,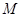 为
为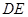 的中点,
的中点,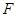 为
为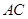 的中点,
的中点,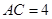 .
.
(1)求证:平面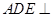 平面
平面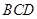 ;
;
(2)求证: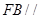 平面
平面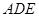 .
.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高三12月月考文科数学试卷(解析版) 题型:解答题
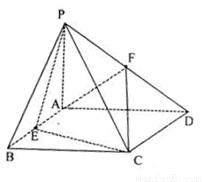
(本小题满分14分)如图,四棱锥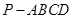 中,
中,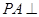 平面
平面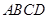 ,四边形
,四边形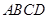 是矩形,
是矩形,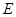 ,
,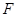 分别是
分别是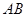 ,
,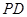 的中点.若
的中点.若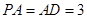 ,
,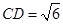 。
。
(1)求证: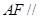 平面
平面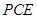 ;
;
(2)求直线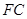 平面
平面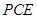 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com