
(1)证明{bn}为等差数列;
(2)求数列{an}的前n项和Sn.
(文)已知数列{an}的前n项和为Sn,且当n∈N*时满足Sn=-3n2+6n,数列{bn}满足bn=(![]() )n-1,数列{cn}满足cn=
)n-1,数列{cn}满足cn=![]() an·bn.
an·bn.
(1)求数列{an}的通项公式an;
(2)求数列{cn}的前n项和Tn.
(理)(1)证明:∵bn=![]()
=![]() +1=bn-1+1(n≥2),
+1=bn-1+1(n≥2),
∴bn-bn-1=1(n≥2).
∴{bn}是公差为1,首项为b1=![]() =2的等差数列.
=2的等差数列.
(2)解:由(1)知bn=2+(n-1)·1=n+1,
即![]() =n+1,∴an=(n+1)2n+1.
=n+1,∴an=(n+1)2n+1.
∴Sn=[2·2+3·22+4·23+…+(n+1)2n]+n.
令Tn=2·2+3·22+…+n·2n-1+(n+1)·2n,
∴2Tn=2·22+…+n·2n+(n+1)2n+1.
∴-Tn=2·2+1·22+…+1·2n-(n+1)2n+1
=4+![]() -(n+1)2n+1
-(n+1)2n+1
=4+2n+1-4-n·2n+1-2n+1=-n·2n+1.
∴Tn=n·2n+1.
∴Sn=n·2n+1+n.
(文)解:(1)当n=1时,a1=S1=3,
当n≥2时,an=Sn-Sn-1=9-6n,
∴an=9-6n.
(2)∵bn=(![]() )n-1,cn=
)n-1,cn=![]() an·bn=
an·bn=![]() ·(
·(![]() )n-1=(3-2n)·(
)n-1=(3-2n)·(![]() )n,
)n,
∴Tn=![]() -(
-(![]() )2-3·(
)2-3·(![]() )3-…-(2n-3)·(
)3-…-(2n-3)·(![]() )n,
)n,
![]() Tn=(
Tn=(![]() )2-(
)2-(![]() )3-…-(2n-5)·(
)3-…-(2n-5)·(![]() )n-(2n-3)(
)n-(2n-3)(![]() )n+1.
)n+1.
∴![]() Tn=
Tn=![]() -2·(
-2·(![]() )2-2·(
)2-2·(![]() )3-…-?2·?(
)3-…-?2·?(![]() )n+(2n-3)·(
)n+(2n-3)·(![]() )n+1
)n+1
=![]() -2·
-2·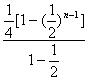 +(2n-3)·(
+(2n-3)·(![]() )n+1,
)n+1,
∴Tn=(2n+1)(![]() )n-1.
)n-1.


科目:高中数学 来源: 题型:
A.nan<Sn<na1 B.Sn<nan<na1 C.nan>Sn>na1 D.Sn>na1>nan
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)判断{![]() }是否为等差数列?并证明你的结论;
}是否为等差数列?并证明你的结论;
(2)求Sn和an;
(3)求证:S12+S22+…+Sn2≤![]()
![]() .
.
(文)数列{an}的前n项和Sn(n∈N*),点(an,Sn)在直线y=2x-3n上.
(1)求证:数列{an+3}是等比数列;
(2)求数列{an}的通项公式;
(3)数列{an}中是否存在成等差数列的三项?若存在,求出一组适合条件的三项;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)若a1=0,求a2、a3的值;
(2)求证:a1=0是数列{an}为等差数列的充要条件.
(文)如图,直线l:y=![]() (x-2)和双曲线C:
(x-2)和双曲线C:![]() =1(a>0,b>0)交于A、B两点,且|AB|=
=1(a>0,b>0)交于A、B两点,且|AB|=![]() ,又l关于直线l1:y=
,又l关于直线l1:y=![]() x对称的直线l2与x轴平行.
x对称的直线l2与x轴平行.

(1)求双曲线C的离心率;
(2)求双曲线C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求证:数列{an+1-an}(n∈N*)是等比数列;
(2)记bn=anln|an|(n∈N*),当t=![]() 时,数列{bn}中是否存在最大项.若存在,是第几项?若不存在,请说明理由.
时,数列{bn}中是否存在最大项.若存在,是第几项?若不存在,请说明理由.
(文)已知等比数列{xn}各项均为不等于1的正数,数列{yn}满足![]() =2(a>0且a≠1),设y3=18,y6=12.
=2(a>0且a≠1),设y3=18,y6=12.
(1)求证:数列{yn}是等差数列;
(2)若存在自然数M,使得n>M时,xn>1恒成立,求M的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求数列{an}的通项公式;
(2)设数列{bn}的前n项和为Tn,且bn=![]() ,求证:对任意正整数n,总有Tn<2;
,求证:对任意正整数n,总有Tn<2;
(3)在正数数列{cn}中,设(cn)n+1=![]() an+1(n∈N*),求数列{lncn}中的最大项.
an+1(n∈N*),求数列{lncn}中的最大项.
(文)已知数列{xn}满足xn+1-xn=(![]() )n,n∈N*,且x1=1.设an=
)n,n∈N*,且x1=1.设an=![]() xn
xn![]() ,且T2n=a1+2a2+3a3+…+ (2n-1)a2n-1+2na2n.
,且T2n=a1+2a2+3a3+…+ (2n-1)a2n-1+2na2n.
(1)求xn的表达式;
(2)求T2n;
(3)若Qn=1![]() (n∈N*),试比较9T2n与Qn的大小,并说明理由.
(n∈N*),试比较9T2n与Qn的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com