练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图所示，O是△ABC的内心，∠BOC=100°，则∠BAC=
     
    度．
    精英家教网
    分析：由三角形内切定义可知：OB、OC是∠ABC、∠ACB的角平分线．利用内角和定理先求得∠OBC+∠OCB=80°，所以可知∠OBC+∠OCB=
    1
    2
    （∠ABC+∠ACB），把对应数值代入此关系式即可求得∠BAC的值．
    解答：解：∵OB、OC是∠ABC、∠ACB的角平分线，
    ∴∠OBC+∠OCB=180°-100°=80°，而∠OBC+∠OCB=
    1
    2
    （∠ABC+∠ACB）=80°，
    ∴∠ABC+∠ACB=160°，
    ∴∠BAC=180°-160°=20°．
    故答案为20．
    点评：本题通过三角形内切圆，考查切线的性质．属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网A．（选修4-4坐标系与参数方程）已知点A是曲线ρ=2sinθ上任意一点，则点A到直线ρsin(θ+
    π3
    )=4    的距离的最小值是
     
    ．
    B．（选修4-5不等式选讲）不等式|x-log2x|＜x+|log2x|的解集是
     
    ．
    C．（选修4-1几何证明选讲）如图所示，AC和AB分别是圆O的切线，且OC=3，AB=4，延长AO到D点，则△ABD的面积是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
    A．（不等式选做题）不等式|2x-1|＜3的解集为
    （-1，2）
    （-1，2）
    ．
    B、（选修4-1几何证明选讲） 如图所示，AC和AB分别是⊙O的切线，且OC=3，AB=4，延长AO到D点，则△ABC的面积是
    192
    25
    192
    25
    ．
    C．（坐标系与参数方程选做题）参数方程
    x=cosα
    y=1+sinα
    （α为参数）化成普通方程为
    x2+（y-1）2=1
    x2+（y-1）2=1
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

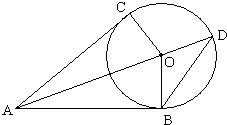    （2011•广东模拟）（几何证明选讲）如图所示，AC和AB分别是圆O的切线，B、C 为切点，且OC=3，AB=4，延长OA到D点，则△ABD的面积是
    48
    5
    48
    5
    ．

    查看答案和解析>>

    科目：高中数学 来源：河南省许昌高级中学2006－2007学年下期期末教学质量评估试卷、高二数学 题型：013

    如图所示，O是半径为1的球心，点A、B、C在球面上，OA、OB、OC两两垂直，E、F分别是大圆弧AB与AC的中点，则点E、F在该球面上的球面距离是(　　)]

    [　　]

    A．

    B．

    C．

    D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，O是线段AB的中点，|AB|＝2c，以点A为圆心，2a为半径作一圆，其中。

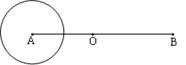
    （1）若圆A外的动点P到B的距离等于它到圆周的最短距离，建立适当坐标系，求动点P的轨迹方程，并说明轨迹是何种曲线；

    （2）经过点O的直线l与直线AB成60°角，当c＝2，a＝1时，动点P的轨迹记为E，设过点B的直线m交曲线E于M、N两点，且点M在直线AB的上方，求点M到直线l的距离d的取值范围。

    查看答案和解析>>

    同步练习册答案