
如图,平面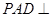 平面
平面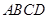 ,
,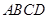 是正方形,
是正方形,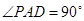 ,且
,且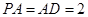 ,
,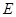 、
、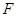 、
、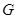 分别是线段
分别是线段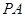 、
、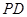 、
、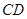 的中点.
的中点.
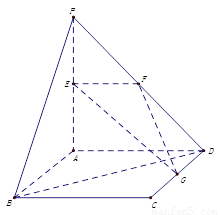
(1)求证: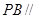 平面
平面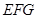 ;
;
(2)求异面直线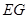 、
、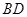 所成角的余弦值.
所成角的余弦值.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
 (2012•河北模拟)如图,直角坐标平面内的正六边形ABCDEF,中心在原点边长为a,AB边平行x轴,直线l:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则关于函数S=f(t)的奇偶性的判断正确的是( )
(2012•河北模拟)如图,直角坐标平面内的正六边形ABCDEF,中心在原点边长为a,AB边平行x轴,直线l:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则关于函数S=f(t)的奇偶性的判断正确的是( )查看答案和解析>>
科目:高中数学 来源: 题型:
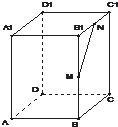 (2013•浦东新区二模)如图,已知正四棱柱ABCD-A1B1C1D1的底面边长是2,体积是16,M,N分别是棱BB1、B1C1的中点.
(2013•浦东新区二模)如图,已知正四棱柱ABCD-A1B1C1D1的底面边长是2,体积是16,M,N分别是棱BB1、B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:

(1)证明AB1∥平面DBC1;
(2)假设AB1⊥BC1,求以BC1为棱,DBC1与CBC1为面的二面角α的度数.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三上学期第三次统练理科数学试卷(解析版) 题型:选择题
如图1所示,正△ABC中,CD是AB边上的高, E、F分别是AC、BC的中点.现将△ACD沿CD折起,使平面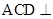 平面BCD(如图2),则下列结论中不正确的是( )
平面BCD(如图2),则下列结论中不正确的是( )
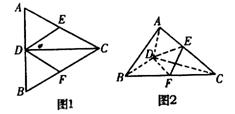
A.AB//平面DEF B.CD⊥平面ABD
C.EF⊥平面ACD D.V三棱锥C—ABD=4V三棱锥C—DEF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com