解:(1)由

,得

<1,
∴-2m
2+m+3>0,解得,-1<m<

,
又∵m∈Z,∴m=0或1
当m=0时,g(x)的底数为1,无意义,舍去.
当m=1时,∴-2m
2+m+3=2,f(x)=x
2是偶函数.此时g(x)的底数为2,成立
综上所述,m的值为1,f(x)=x
2(2)由(1)知,

,(x≠2)
由
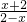
>0,得-2<x<2,∴g(x)的定义域为(-2,2)
设-2<x
1<x
2<2,f(x
1)-f(x
2)=

=log
a
•

=log
a
∵-2<x
1<x
2<2,∴0<-x
1x
2+2x
1-2x
2+4<4-2x
1+2x
2-x
1x
2?

<1
∴log
a
<0
∴函数g(x)在(-2,2)上为增函数.
分析:(1)利用

,解指数不等式,即可求出m的范围,再根据m∈Z,的到整数m,代入两个函数,判断是否成立,就可求出m的值,并可判断f(x)的奇偶性.
(2)用定义法判断函数g(x)的单调性,先求出函数的定义域,再设函数在定义域上任意两个x
1,x
2,且x
1<x
2,再作差比较f(x
1)与f(x
2)的大小即可,作差后一定要将差分解为几个因式的乘积的形式,再判断每一个因式的符号,根据负因式的个数判断积的符号,最后得出结论.
点评:本题主要考查了函数的奇偶性与单调性的判断,属于概念考查题.

 .
. ,得
,得 <1,
<1, ,
, ,(x≠2)
,(x≠2)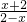 >0,得-2<x<2,∴g(x)的定义域为(-2,2)
>0,得-2<x<2,∴g(x)的定义域为(-2,2)
 •
• =loga
=loga
 <1
<1 <0
<0 ,解指数不等式,即可求出m的范围,再根据m∈Z,的到整数m,代入两个函数,判断是否成立,就可求出m的值,并可判断f(x)的奇偶性.
,解指数不等式,即可求出m的范围,再根据m∈Z,的到整数m,代入两个函数,判断是否成立,就可求出m的值,并可判断f(x)的奇偶性.
