练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    试判断方程x3+x2-5x-5=0的解的个数.

    分析：本题考查导数的应用.要判断方程根的个数，可把方程视作函数，由导数确定它的单调区间，描绘出它的大致图象，再由根的存在性定理，确定方程根的个数.

    解：不妨设f(x)=x3+x2-5x-5,

    则f′(x)=3x2+2x-5=(3x+5)(x-1).

    令f′(x)>0，得x<-或x>1;

    f′(x)<0，得-<x<1.

    故函数f(x)在区间(-∞,-)，（1，+∞）上是增函数;

    在区间(-,1)上是减函数.

    它的大致图象是：

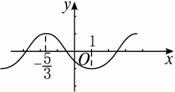
    显然方程x3+x2-5x-5=0的根有3个.

    此外,本题也可通过因式分解求解.

    点评 利用导数可判断方程根的个数:若函数y=f(x)在(a,b)上是单调函数,且f(a)·f(b)<0,则必存在一个x0,使得f(x0)=0.依据根的分布的基本原理,结合函数的导数可完成对方程根的个数的判断.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知二次函数f(x)=ax2+bx+1和g(x)=
    bx-1a2x+2b

    （1）f（x）为偶函数，试判断g（x）的奇偶性；
    （2）若方程g（x）=x有两个不相等的实根，当a＞0时判断f（x）在（-1，1）上的单调性；
    （3）若方程g（x）=x的两实根为x1，x2f（x）=0的两根为x3，x4，求使x3＜x1＜x2＜x4成立的a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知两个二次函数：y=f（x）=ax2+bx+1与y=g（x）=a2x2+bx+1，函数y=g（x）图象与x轴有两个交点，其横坐标分别为x1，x2（x1＜x2）．
    （1）证明：y=f（x）在（-1，1）上是单调函数；
    （2）当a＞1时，设x3，x4是方程ax2+bx+1=0的两实根，且x3＜x4，当a＞1时，试判断x1，x2，x3，x4的大小关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=ex（x3-6x2+3x+a），
    （Ⅰ）当a=1时，求函数在（0，f（0））处的切线方程；
    （Ⅱ）若函数f（x）有三个极值点，求实数a的取值范围；
    （Ⅲ）定义：如果曲线C上存在不同点的两点A（x1，y1 ），B（x2，y2 ），过AB的中点且垂直于x轴的直线交曲线C于点M，使得直线AB与曲线C在M处的切线平行，则称曲线C有“平衡切线”．
    试判断函数G（x）=[f'（x）-f（x）]•e-x+ex的图象是否有“平衡切线”，为什么？

    查看答案和解析>>

    科目：高中数学 来源：山东省临祈市2006—2007学年度上学期高三年级期中统一考试　数学试题(理) 题型：044

    解答题：解答应写出文字说明，证明过程或演算步骤．

    已知两个二次函数：y＝f(x)＝ax2＋bx＋1与y＝g(x)＝a2x2＋bx－1(a＞0)，函数y＝g(x)的图像与x轴有两个交点，其交点横坐标分别为x1，x2(x1＜x2)

    (1)

    试证：y＝f(x)在(－1，1)上是单调函数

    (2)

    当a＞1时，设x3，x4是方程ax2＋bx＋1＝0的两实根，且x3＞x4，试判断x1，x2，x3，x4的大小关系

    查看答案和解析>>

    同步练习册答案