已知数列{an}的前n项和为Sn,a1=1,且3an+1+2Sn=3(n∈N+).
(I) 求a2,a3的值,并求数列{an}的通项公式;
(II)若对任意正整数n,k≤Sn恒成立,求实数k的最大值.
解:(I)∵a
1=1,且3a
n+1+2s
n=3(n∈N
+)
∴当n=1时,3a
2+2a
1=3,∴
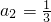
)
∴当n=2时,3a
3+2(a
1+a
2)=3,∴

∵3a
n+1+2s
n=3①
∴当n≥2时,3a
n+2s
n-1=3 ②
由①-②,得3a
n+1-3a
n+2a
n=0
∴

,
又∵
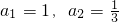
,
∴数列{a
n}是首项为1,公比为

的等比数列.
∴

(II)由(I)知

由题意可知,对于任意的正整数n,恒有

令f(n)=

,则函数为单调增函数,∴当n=1时,f(n)
min=1
∴必有k≤1,即实数k的最大值为1.
分析:(I)利用a
1=1,且3a
n+1+2s
n=3(n∈N
+),令n=1、2,可求a
2,a
3的值,n≥2时,3a
n+2s
n-1=3与条件相减,可得数列{a
n}是首项为1,公比为

的等比数列,从而可求数列{a
n}的通项公式;
(II)求出等比数列的和,求出数列和的最小值,即可得到实数k的最大值.
点评:本题考查数列的通项与求和,考查恒成立问题,解题的关键是利用等比数列的定义,确定函数的单调性.

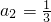 )
)
 ,
,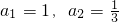 ,
, 的等比数列.
的等比数列.


 ,则函数为单调增函数,∴当n=1时,f(n)min=1
,则函数为单调增函数,∴当n=1时,f(n)min=1  的等比数列,从而可求数列{an}的通项公式;
的等比数列,从而可求数列{an}的通项公式;
