
分析 根据几何体作出轴截面,由图和题意列出圆锥的半径和正方体棱长的关系式,求出它们的长度关系,再代入对应的面积公式,求出表面积值.
解答  解:作出几何体的轴截面如图:
解:作出几何体的轴截面如图:
由题意圆锥的底面半径为r,母线长l=3r,
则圆锥的高h=2$\sqrt{2}$r,设正方体的棱长为a,
由轴截面得,$\frac{h-a}{h}$=$\frac{\sqrt{2}a}{2r}$,解得a=$\frac{2\sqrt{2}r}{3}$,
则该正方体的表面积为6a2=6×$\frac{8}{9}$r2=$\frac{16{r}^{2}}{3}$,
故答案为:$\frac{16{r}^{2}}{3}$.
点评 本题考查了利用几何体的轴截面分析量的等量关系,注意不同量的转化,考查了空间想象能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{13}$ | B. | $\frac{5}{12}$ | C. | $\frac{13}{12}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
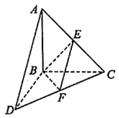 如图,三棱锥A-BCD中,△ABC和△BCD所在平面互相垂直,且AB=CD=4,AC=4$\sqrt{2}$,CD=4$\sqrt{3}$,∠ACB=45°,E,F分别为MN的中点.
如图,三棱锥A-BCD中,△ABC和△BCD所在平面互相垂直,且AB=CD=4,AC=4$\sqrt{2}$,CD=4$\sqrt{3}$,∠ACB=45°,E,F分别为MN的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com