
f(x)=x2-4x-4,x∈[t,t+1],t∈R,求:
(1)f(x)的最小值g(t)的解析式;
(2)求g(t)的最小值.
|
解:(1)∵f(x)=(x-2)2-8,∴f(x)的对称轴是直线x=2. 当2∈[t,t+1],即t≤2≤t+1时,1≤t≤2,g(t)=f(2)=-8; 当2>t+1,即t<1时,f(x)在[t,t+1]上随x增大f(x)减小. ∴g(t)=f(t+1)=t2-2t-7. 当t>2时,f(x)在[t,t+1]上随x增大f(x)增大, ∴g(t)=f(t)=t2-4t-4. 综上可得g(t)=t (2)当t<1时,g(t)=t2-2t-7=(t-1)2-8>-8; 当1≤t≤2时,g(t)=-8; 当t>2时,g(t)=t2-4t-4=(t-2)2-8>-8, 则g(t)的最小值是-8. |
|
(1)易得函数的对称轴为x=2,之后分对称轴在区间[t,t+1]左、内、右分段得出最小值的解析式.(2)g(t)是分段函数,各段上最小值中的最小值是g(t)的最小值. |


科目:高中数学 来源: 题型:
给出下列四个命题:①函数f(x)=3x-6的零点是2;②函数f(x)=x2+4x+4的零点是-2;③函数f(x)=log3(x-1)的零点是1;④函数f(x)=2x-1的零点是0.其中正确的个数为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=x2-4x+3,g(x)=3x-2,集合M={x∈R|f(g(x))>0},N={x∈R|g(x)<2},则M∩N为 ( )
A.(1,+∞) B.(0,1)
C.(-1,1) D.(-∞,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
若函数f(x)的导函数f′(x)=x![]() 2-4x+3,则函数f(x+1)的单调递减区间是 ( )
2-4x+3,则函数f(x+1)的单调递减区间是 ( )
A.(2,4) B.(-3,-1)
C.(1,3) D.(0,2)
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修1单调性与最大(小)值练习卷(二)(解析版) 题型:选择题
函数f(x)=x2-4x+5在区间[0,m]上的最大值为5,最小值为1,则m的取值范围是( )
A.[2,+∞) B.[2,4]
C.(-∞,2] D.[0,2]
查看答案和解析>>
科目:高中数学 来源:2013届四川省成都外国语学校高二下学期期中考试数学试卷(解析版) 题型:解答题
(本题满分12分)设命题p:函数 是R上的减函数,命题q:函数f(x)=x2-4x+3在
是R上的减函数,命题q:函数f(x)=x2-4x+3在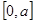 上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求
上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com