Question

设f（x）=2x³+ax²+bx+1的导数为f'（x），若函数y=f'（x）的图象关于直线x=﹣对称，且f'（1）=0
（Ⅰ）求实数a，b的值
（Ⅱ）求函数f（x）的极值．

Answer 1

解：（Ⅰ）因f（x）=2x³+ax²+bx+1，
故f '（x）=6x²+2ax+b
从而f '（x）=6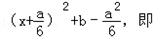
y=f '（x）关于直线x=﹣对称，
从而由条件可知﹣=﹣，
解得a=3
又由于f '（x）=0，
即6+2a+b=0，
解得b=﹣12
（Ⅱ）由（Ⅰ）知f（x）=2x³+3x²﹣12x+1
f '（x）=6x²+6x﹣12
=6（x﹣1）（x+2）
令f '（x）=0，得x=1或x=﹣2
当x∈（﹣∞，﹣2）时，f '（x）＞0，f（x）在（﹣∞，﹣2）上是增函数；
当x∈（﹣2，1）时，f '（x）＜0，f（x）在（﹣2，1）上是减函数；
当x∈（1，+∞）时，f '（x）＞0，f（x）在（1，+∞）上是增函数．
从而f（x）在x=﹣2处取到极大值f（﹣2）=21，在x=1处取到极小值f（1）=﹣6．