
分析 由两角和的正弦函数公式,诱导公式化简函数可得f(x)=-sinx,由正弦函数的图象和性质即可得解.
解答 解:∵f(x)=sin(x+$\frac{3π}{4}$)+cos(x+$\frac{3π}{4}$)=$\sqrt{2}$[$\frac{\sqrt{2}}{2}$sin(x+$\frac{3π}{4}$)+$\frac{\sqrt{2}}{2}$cos(x+$\frac{3π}{4}$)]=$\sqrt{2}$sin(x+π)=-$\sqrt{2}$sinx.
∴周期T=$\frac{2π}{1}=2π$,由正弦函数的图象和性质可得此函数为奇函数.
故答案为:2π,奇.
点评 本题主要考查了两角和的正弦函数公式,诱导公式,正弦函数的图象和性质,属于基本知识的考查.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}×\frac{1}{4}$ | B. | ($\frac{5}{9}$)3×$\frac{4}{9}$ | C. | 4×($\frac{5}{9}$)3×$\frac{4}{9}$ | D. | 4×($\frac{4}{9}$)3×$\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {y=sinx} | B. | {x|-1≤x≤1} | C. | {x|x=2π} | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
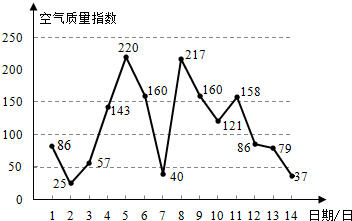
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com