已知函数f(x)=2x3-ax2+6bx在x=1处有极大值7.
(1)求f(x)的解析式及单调区间;
(2)求f(x)在[-3,3]上的最大值和最小值.
【答案】
分析:(1)对f(x)进行求导,根据函数f(x)=2x
3-ax
2+6bx在x=1处有极大值7,可得f′(-1)=0,f(-1)=7,从而求出a和b,求出f(x)的解析式,再利用导数研究其单调性;
(2)由(1)已知f(x)的单调区间,令f′(x)=0,求出极值点,得到极大值和极小值,可以利用导数研究其最值问题;
解答:解:(1)f′(x)=6x
2-2ax+6b,…(1分)
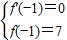
…(2分)⇒
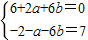
⇒
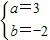
,…(3分)
∴f(x)=2x
3-3x
2-12x. …(4分)
又∵f′(x)=6x
2-6x-12,由f′(x)>0得6x
2-6x-12>0解得x<-1或x>2(5分)
由f′(x)<0得6x
2-6x-12<0,解得-1<x<2 …(6分)
∴f(x)的单调增区间为(-∞,-1),(2,+∞),…(7分)
f(x)的单调减区间为(-1,2). …(8分)
(2)f′(x)=0得x=-1和x=2
则f(x)在[-3,3]的变化情况如下表
| x | -3 | (-3,-1) | -1 | (-1,2) | 2 | (2,3) | 3 |
| f′(x) | | + | | - | | + | |
| f(x) | -45 | ↗ | 7 | ↘ | -20 | ↗ | -9 |
由表知f(x)在[-3,3]上的最大值和最小值分别为7,-45 …(13分)
点评:此题主要考查利用导数研究函数的单调性及其应用,也考查极大值和极小值与最大值和最小值的区别,是一道中档题;

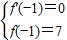 …(2分)⇒
…(2分)⇒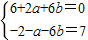
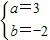 ,…(3分)
,…(3分)

 名校课堂系列答案
名校课堂系列答案