练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (理)数列1，2，1，2，2，1，2，2，2，1，2，2，2，2，1，2，……，其相邻的两个1被2隔开，第n对1之间有n个2，则数列的前1234项的和为

    [　　]

    A．2450

    B．2419

    C．4919

    D．1234

    答案：B
    解析：

    设该数列前1234项中共有k个1，则可得k＝49．∴所求的和为49+2(1234－49)＝2419，或构造补数列1，0，1，0，0，1，0，0，0，1，0，0，0，0，1，0……，显然其与原数列相应项之和均为2，故所求和为1234x2－49＝2419


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知正项数列{an}满足：an+1=
    1
    2
    （an+
    1
    an
    ）（n∈N+）．
    （1）求a1的范围，使得an+1＜an恒成立；
    （2）若a1=
    3
    2
    ，证明an＜1+
    1
    2n+1
    （n∈N+，n≥2）；
    （3）（理）若a1=
    3
    2
    ，证明：
    a1
    a2
    +
    a2
    a3
    +
    a3
    a4
    +…+
    an
    an+1
    -n＜
    		2
    +1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （06年上海卷理）（16分）

    已知有穷数列共有2项（整数≥2），首项＝2．设该数列的前项和为，且＝＋2（＝1，2，┅，2－1），其中常数＞1．

    （1）求证：数列是等比数列；

    （2）若＝2，数列满足＝（＝1，2，┅，2），求数列的通项公式；

    （3）若（2）中的数列满足不等式|－|＋|－|＋┅＋|－|＋|－|≤4，求的值．

    查看答案和解析>>

    科目：高中数学 来源：2006年广东省高考数学试卷（解析版） 题型：解答题

    已知公比为q（0＜q＜1）的无穷等比数列{an}各项的和为9，无穷等比数列{an2}各项的和为．
    （1）求数列{an}的首项a1和公比q；
    （2）对给定的k（k=1，2，3，…，n），设T（k）是首项为ak，公差为2ak-1的等差数列，求T（2）的前2007项之和；
    （3）（理）设bi为数列T（i）的第i项，Sn=b1+b2+…+bn：
    ①求Sn的表达式，并求出Sn取最大值时n的值．
    ②求正整数m（m＞1），使得存在且不等于零．
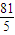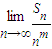    （文）设bi为数列T（i）的第i项，Sn=b1+b2+…+bn：求Sn的表达式，并求正整数m（m＞1），使得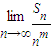存在且不等于零．

    查看答案和解析>>

    科目：高中数学 来源：2009-2010年上海市华东师大二附中高三数学综合练习试卷（09）（解析版） 题型：解答题

    已知公比为q（0＜q＜1）的无穷等比数列{an}各项的和为9，无穷等比数列{an2}各项的和为．
    （1）求数列{an}的首项a1和公比q；
    （2）对给定的k（k=1，2，3，…，n），设T（k）是首项为ak，公差为2ak-1的等差数列，求T（2）的前2007项之和；
    （3）（理）设bi为数列T（i）的第i项，Sn=b1+b2+…+bn：
    ①求Sn的表达式，并求出Sn取最大值时n的值．
    ②求正整数m（m＞1），使得存在且不等于零．
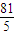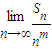    （文）设bi为数列T（i）的第i项，Sn=b1+b2+…+bn：求Sn的表达式，并求正整数m（m＞1），使得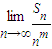存在且不等于零．

    查看答案和解析>>

    同步练习册答案