Question

在△ABC中，若tanA∶tanB=a²∶b²,试判断△ABC的形状.

Answer 1

分析：可从问题已知条件出发，寻找到三角形的边与边或角与角之间的关系，然后判断.

解法一:由同角三角函数关系及正弦定理可推得=,

∵A,B为三角形的内角,∴sinA≠0,sinB≠0.

∴.∴sin2A=sin2B.

∴2A=2B或2A=π-2B.

∴A=B或A+B=.

∴△ABC为等腰三角形或直角三角形.

解法二：由已知和正弦定理可得：

.

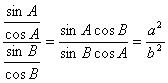由正弦定理和余弦定理得,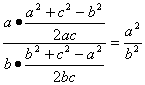

整理得a⁴-a²c²+b²c²-b⁴=0,

即(a²-b²)(a²+b²-c²)=0.∴a²=b²或a²+b²-c²=0.∴a=b或a²+b²=c².

∴△ABC是等腰三角形或直角三角形.

温馨提示

    已知三角形中的边角关系式，判断三角形的形状，有两条思考路线：（1）化边为角,再进行三角恒等变换求出三个角之间的关系式；

（2）化角为边，再进行代数恒等变换求出三条边之间的关系式，两种转化主要应用正弦定理和余弦定理.