
椭圆E: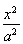 +
+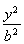 =1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3.
=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3.
(1)求椭圆E的方程;
(2)若过F1的直线l交椭圆于A,B两点,判断是否存在直线l使得∠AF2B为钝角,若存在,求出l的斜率k的取值范围.
(1) 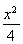 +
+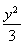 =1 (2)存在,斜率k的取值范围为-
=1 (2)存在,斜率k的取值范围为-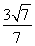 <k<
<k<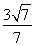
【解析】
解:(1)依题意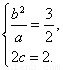
解得a2=4,b2=3,
∴椭圆的方程为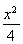 +
+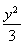 =1.
=1.
(2)①当过F1的直线AB的斜率不存在时,
不妨取A(-1,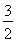 ),B(-1,-
),B(-1,-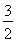 )
)
则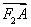 ·
·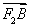 =
=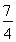 ,显然∠AF2B不为钝角.
,显然∠AF2B不为钝角.
②直线l的斜率为k,l方程为y=k(x+1),
由
消去y,整理得(3+4k2)x2+8k2x+4k2-12=0.
∵直线l与椭圆交于两点,
∴Δ=(8k2)2-4(3+4k2)(4k2-12)=4×36(k2+1)>0.
设A(x1,y1),B(x2,y2),
则x1+x2=-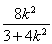 ,x1·x2=
,x1·x2=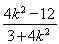 .
.
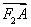 =(x1-1,y1),
=(x1-1,y1),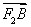 =(x2-1,y2).
=(x2-1,y2).
∵∠AF2B为钝角,
∴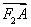 ·
·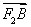 <0.
<0.
即(x1-1)(x2-1)+y1y2<0,
整理得(k2+1)x1x2+(k2-1)(x1+x2)+k2+1<0.
即(k2+1)·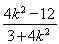 -(k2-1)·
-(k2-1)·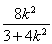 +k2+1<0,
+k2+1<0,
整理得7k2<9,
解得-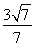 <k<
<k<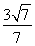 .
.
∴存在满足条件的直线l,
其斜率k的取值范围为-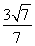 <k<
<k<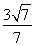 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
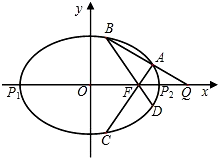 (2013•宁波二模)如图,已知椭圆E:
(2013•宁波二模)如图,已知椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 1 |
| |P1Q| |
| 1 |
| |P2Q| |
| 2 |
| |FQ| |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练24练习卷(解析版) 题型:解答题
已知椭圆E: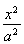 +
+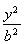 =1(a>b>0),以抛物线y2=8x的焦点为顶点,且离心率为
=1(a>b>0),以抛物线y2=8x的焦点为顶点,且离心率为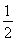 .
.
(1)求椭圆E的方程;
(2)若F为椭圆E的左焦点,O为坐标原点,直线l:y=kx+m与椭圆E相交于A、B两点,与直线x=-4相交于Q点,P是椭圆E上一点且满足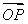 =
=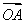 +
+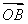 ,证明
,证明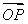 ·
·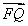 为定值,并求出该值.
为定值,并求出该值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练22练习卷(解析版) 题型:选择题
设F1,F2是椭圆E: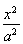 +
+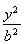 =1(a>b>0)的左、右焦点,P为直线x=
=1(a>b>0)的左、右焦点,P为直线x=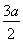 上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
(A) 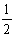 (B)
(B) 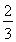 (C)
(C) 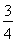 (D)
(D) 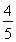
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)若F2(2,0)关于直线y=![]() x+
x+![]() 的对称点在椭圆E上,求该椭圆E的方程;
的对称点在椭圆E上,求该椭圆E的方程;
(2)若椭圆E的内接平行四边形的一组对边分别经过它的两个焦点(如图),求这个平行四边形面积的最大值.
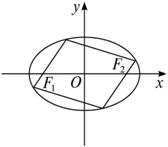
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com