练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    当n＞2时，求证：logn(n-1)logn(n+1)＜1.

    答案：
    解析：

    		 思路分析：不等式左边含有不确定字母n，两个对数式底数相同，真数中没有常数项，而右边为常数1，应考虑应用基本不等式逐步放缩证明，采用放缩法证明较好.

    证明：∵n＞2，∴logn(n-1)＞0,logn(n+1)＞0.

    ∴logn(n-1)logn(n+1)＜［］2=［］2

    ＜［］2=1.

    ∴n＞2时,logn(n-1)logn(n+1)＜1.

    方法归纳

    在用放缩法证明不等式A≤B时，我们找一个(或多个)中间量C作比较，即若能断定A≤C与C≤B同时成立，那么A≤B显然正确.所谓的“放”即把A放大到C，再把C放大到B;反之，所谓的“缩”即由B缩到C，再把C缩到A.同时在放缩时必须时刻注意放缩的跨度，放不能过头，缩不能不及.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2013•温州二模）己知数列{an}的前n项和为Sn，a1=2．当n≥2时．Sn-1+l，an．Sn+1成等差数列．
    （I）求证：{Sn+1}是等比数列：
    （II）求数列{nan}的前n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图在直角坐标系xoy中，圆O与x轴交于A、B两点，且|AB|=4，定直线l垂直于x轴正半轴，且到圆心O的距离为4，点P是圆O上异于A、B的任意一点，直线PA、PB分别交l于点M、N．
    （1）若∠PAB=30°，求以MN为直径的圆的方程；
    （2）当点P变化时，求证：以MN为直径的圆必过圆O内一定点．

    查看答案和解析>>

    科目：高中数学 来源：上海市十校2012届高三第二次联考数学文科试题 题型：044

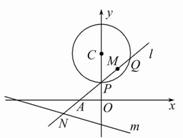
    已知过点A(－1，0)的动直线l与圆C：x2＋(y－3)2＝4相交于P，Q两点，M是PQ中点，l与直线m：x＋3y＋6＝0相交于N．

    (1)求证：当l与m垂直时，l必过圆心C；

    (2)当PQ＝2时，求直线l的方程；

    (3)探索是否与直线l的倾斜角有关？若无关，请求出其值；若有关，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：上海市十校2012届高三第二次联考数学理科试题 题型：044

    已知过点A(－1，0)的动直线l与圆C：x2＋(y－3)2＝4相交于P，Q两点，M是PQ中点，l与直线m：x＋3y＋6＝0相交于N．

    (1)求证：当l与m垂直时，l必过圆心C；

    (2)当PQ＝2时，求直线l的方程；

    (3)探索是否与直线的倾斜角有关？若无关，请求出其值；若有关，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知过点A(－1,0)的动直线l与圆C：x2＋(y－3)2＝4相交于P，Q两点，M是PQ中点，l与直线m：x＋3y＋6＝0相交于N.

    (1)求证：当l与m垂直时，l必过圆心C；

    (2)当PQ＝2时，求直线l的方程；

    (3)探索是否与直线l的倾斜角有关？若无关，请求出其值；若有关，请说明理由.

    查看答案和解析>>

    同步练习册答案