练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
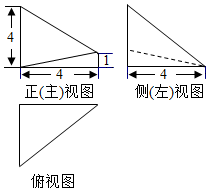
    19．已知某几何体的三视图（如图），其中俯视图和侧（左）视图都是腰长为4的等腰直角三角形，正（主）视图为直角梯形，则此几何体的体积V的大小为（　　）
    A．$\frac{35}{3}$B．12C．16D．$\frac{40}{3}$

    分析 由三视图知几何体为四棱锥，其直观图如图所示，即可得出．

    解答 解：由三视图知几何体为四棱锥，其直观图如图：
    四棱锥的高为4，底面为直角梯形的面积S=$\frac{1+4}{2}$×4=10，
    ∴几何体的体积V=$\frac{1}{3}$×10×4=$\frac{40}{3}$．
    故选：D．

    点评 本题考查了三视图的有关计算，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

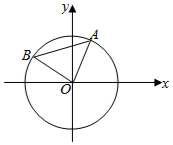    9．A、B是单位圆O上的动点，且A、B分别在第一、二象限．C是圆O与x轴正半轴的交点，△AOB为正三角形．记∠AOC=α．
    （Ⅰ）若A点的坐标为$（\frac{3}{5}，\frac{4}{5}）$．求$\frac{{{{sin}^2}α+sin2a}}{{{{cos}^2}α+cos2α}}$的值；
    （Ⅱ）求|BC|2的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知函数f（x）=$\left\{{\begin{array}{l}{x（x+4），x≥0}\\{x（x-4），x＜0}\end{array}}$，若f（a）＞f（8-a），则a的取值范围是（　　）
    A．（-∞，4）B．（-4，0）C．（0，4）D．（4，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．某城市理论预测2014年到2018年人口总数y （单位：十万）与年份（用2014+x表示）的关系如表所示：
    年份中的x01234
    人口总数y5781119
    （1）请画出上表数据的散点图；
    （2）请根据上表提供的数据，用最小二乘法求出y关于x的回归方程$\stackrel{∧}{y}$=bx+a；
    （3）据此估计2019年该城市人口总数．
    （参考数据：0×5+1×7+2×8+3×11+4×19=132，02+12+22+32+42=30）
    参考公式：线性回归方程为$\hat y=bx+a$，其中 $b=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．先后任意地抛一枚质地均匀的正方体骰子两次，所得点分别记为a和b，则函数f（x）=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+bx存在极值的概率为（　　）
    A．$\frac{13}{36}$B．$\frac{17}{36}$C．$\frac{19}{36}$D．$\frac{23}{36}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知半径为$\frac{2\sqrt{3}}{3}$的球内接一个圆锥，圆锥的轴截面SAB是等边三角形，O1为圆锥底面直径AB的中点，O为球心，动点P在圆锥底面内（包括圆周）运动，若AO⊥OP，则点P形成的轨迹的长度为$\frac{4\sqrt{2}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．设函数f（x）=$\frac{2}{3}$+$\frac{1}{x}$（x＞0），数列{an}满足a1=1，an=f（$\frac{1}{{a}_{n-1}}$），n∈N*，且n≥2
    （1）求数列{an}的通项公式；
    （2）对n∈N*，设Sn=$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$+$\frac{1}{{a}_{3}{a}_{4}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$，若Sn≥$\frac{3t}{4n}$恒成立，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知数列{an}是等比数列．
    （1）设a1=1，a4=8．
    ①若$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2n}}$=M（$\frac{1}{{a}_{1}^{2}}$+$\frac{1}{{a}_{2}^{2}}$+…+$\frac{1}{{a}_{n}^{2}}$），n∈N*，求实数M的值；
    ②若在$\frac{1}{{a}_{1}}$与$\frac{1}{{a}_{4}}$中插入k个数b1，b2，…，bk，使$\frac{1}{{a}_{1}}$，b1，b2，…，bk，$\frac{1}{{a}_{4}}$，$\frac{1}{{a}_{5}}$成等差数列，求这k个数的和Sk；
    （2）若一个数列{cn}的所有项都是另一个数列{dn}中的项，则称{cn}是{dn}的子数列，已知数列{bn}是公差不为0的等差数列，b1=a1，b2=a2，bm=a3，其中m是某个正整数，且m≥3，求证：数列{an}是{bn}的子数列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．若数列{an}是等差数列，首项a1＞0，a2015•a2016＜0，a2015+a2016＞0，使前n项和Sn＞0成立最大自然数n是（　　）
    A．4 029B．4 030C．4 031D．4 032

    查看答案和解析>>

    同步练习册答案