
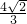 ),N(-
),N(- ,
, )两点.
)两点. ?
? ,即椭圆方程为
,即椭圆方程为 +
+ =1.
=1. +
+ =1,得y2=4(1-
=1,得y2=4(1- )
) )=
)= (x-
(x- a)2+4-
a)2+4- a2(|x|≤3),
a2(|x|≤3), |≤3即0<a≤
|≤3即0<a≤ 时,|AP|2的最小值为4-
时,|AP|2的最小值为4- a2
a2 a2=1?a=±
a2=1?a=± ∉(0,
∉(0, ]
] a>3即
a>3即 <a<3,此时当x=3时,|AP|2的最小值为(3-a)2
<a<3,此时当x=3时,|AP|2的最小值为(3-a)2 ,求出m,n后就得到椭圆的方程.
,求出m,n后就得到椭圆的方程. +
+ =1,得y2=4(1-
=1,得y2=4(1- ),结合题设条件能够推导出|AP|2=
),结合题设条件能够推导出|AP|2= (x-
(x- a)2+4-
a)2+4- a2(|x|≤3),由此可以求出a的值及点P的坐标.
a2(|x|≤3),由此可以求出a的值及点P的坐标.

 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com