
| A. | α≤β<π | B. | α≤β≤π-α | C. | $\frac{π}{2}-α≤β<π$ | D. | $\frac{π}{2}-α≤β≤π-α$ |
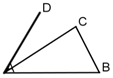
分析 如图所示,图一:过点D作DO⊥平面ABC,垂足为O点,
连接OA,过点O作OE⊥AB,垂足为E点,连接DE.则∠OAD是线段DA和平面ABC所成角α(0<α<$\frac{π}{2}}$),
∠OED是二面角D-AB-C的平面角β,利用直角三角形边角关系即可得出.α<β<π-α.同理图二中:可得α<π-β,α
解答 解:如图所示,
图一:过点D作DO⊥平面ABC,垂足为O点,
连接OA,过点O作OE⊥AB,垂足为E点,连接DE.
则∠OAD是线段DA和平面ABC所成角α(0<α<$\frac{π}{2}}$),
∠OED是二面角D-AB-C的平面角β,
则tanα=$\frac{OD}{OA}$,tanβ=$\frac{OD}{OE}$,OA>OE,
∴tanα<tanβ,可得α<β,α+β<π,因此α<β<π-α.
同理图二中:tanα=$\frac{OD}{OA}$,tan(π-β)=$\frac{OD}{OE}$,
可得α<π-β,α<β,因此α<β<π-α.
综上可得:α<β<π-α.
故选:B.
点评 本题考查了空间位置关系、空间角、直角三角形的边角关系,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{1}{2},0})∪[{1,\frac{3}{2}})$ | B. | $({-\frac{1}{2},\frac{3}{2}})$ | C. | $({-\frac{1}{2},0}]∪[{1,\frac{3}{2}})$ | D. | (-∞,0]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{{\sqrt{2}}}{2})$ | B. | $(\frac{{\sqrt{2}}}{2},1)$ | C. | $(1,\sqrt{2})$ | D. | $\sqrt{2},2)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
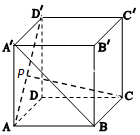 如图,在正方体ABCD-A'B'C'D'中,点P在线段AD'上,且AP≤$\frac{1}{2}$AD'则异面直线CP与BA'所成角θ的取值范围是[$\frac{π}{6}$,$\frac{π}{3}$].
如图,在正方体ABCD-A'B'C'D'中,点P在线段AD'上,且AP≤$\frac{1}{2}$AD'则异面直线CP与BA'所成角θ的取值范围是[$\frac{π}{6}$,$\frac{π}{3}$].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,2} | B. | {0,2} | C. | {2} | D. | {0,-2,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com