练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f(x)在R上单调递增，且满足f(－x)=－f(x),若x+y>0,则f(x)+f(y)的符号是否确定？反过来，若f(x)+

    f(y)>0,则x+y是否一定大于零？

    解:∵x+y>0,∴x>－y.

    ∴f(x)>f(－y).

    又f(x)满足f(－x)=－f(x),

    ∴f(－y)=－f(y).∴f(x)>－f(y).

    即f(x)+f(y)>0,故f(x)+f(y)的符号为正.

    反过来，由于f(x)+f(y)>0,则得f(x)>－f(y)=f(－y).

    又f(x)在R上递增，∴x>－y,即x+y>0.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：随堂练1＋2　讲·练·测　高中数学·必修1（苏教版） 苏教版 题型：022

    下列论断

    ①函数y＝2x2＋x＋1在(0，＋∞)上不是增函数

    ②函数y＝在(－∞，－1)∪(－1，＋∞)上是减函数

    ③函数y＝的单调减区间为[－2，＋∞)

    ④已知f(x)是R上增函数，若a＋b＞0，则f(a)＋f(b)＞f(－a)＋f(－b)其中正确的序号为________．

    查看答案和解析>>

    科目：高中数学 来源：湖南省长郡中学2012届高三第二次月考数学文科试题(人教版) 人教版 题型：044

    已知f(x)是R上的单调函数，且对任意的实数a∈R，有f(a)＋f(－a)＝O恒成立，若f(－3)＝2．

    (1)试判断f(X)在R上的单调性，并说明理由；

    (2)解关于x的不等式：f()＋f(m)＜0，其中m∈R且m＞0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年新建二中模拟文） (12分)    已知是定义在R上的函数，其图象交x轴于A、B、C三点．若点B的坐标为 (2，0)，且f (x) 在[－1，0]和[4，5]上有相同的单调性，在[0，2]和[4，5]上有相反的单调性．
    　　(1)求c的值；
    　　(2)在函数f (x)的图象上是否存在一点M(x0，y0)，使得f (x)在点M的切线斜率为3b？若存在，求出点M的坐标；若不存在，请说明理由；
    　　(3)求| AC |的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知定义在实数集上的函数y=f(x)满足条件:对于任意的x、y∈R, f(x+y)=f(x)+f(y).

    (1)求证:f(0)=0;

    (2)求证:f(x)是奇函数,试举出两个这样的函数;

    (3)若当x＞0时,f(x)＜0.

    ①试判断函数f(x)在R上的单调性,并证明之;

    ②判断函数|f(x)|=a所有可能的解的个数,并求出对应的a的范围.

    查看答案和解析>>

    科目：高中数学 来源：2010届浙江省高一上学期数学期中试卷 题型：填空题

     

    已知函数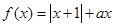  (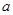∈R). 若函数 f(x)在 R 上具有单调性，则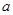的取值范围为_________________.

     

    查看答案和解析>>

    同步练习册答案