
分析 由题意得,直线过圆心(2,1),即 a+b=1,$\frac{1}{a}$+$\frac{2}{b}$=(a+b)($\frac{1}{a}$+$\frac{2}{b}$)=3+$\frac{b}{a}$+$\frac{2a}{b}$,利用基本不等式求出其最小值.
解答 解:由题意得,直线过圆心(2,1),所以,a+b=1.
∴$\frac{1}{a}$+$\frac{2}{b}$=(a+b)($\frac{1}{a}$+$\frac{2}{b}$)=3+$\frac{b}{a}$+$\frac{2a}{b}$≥3+2$\sqrt{2}$,当且仅当$\frac{b}{a}$=$\frac{2a}{b}$时,等号成立,
故答案为3+2$\sqrt{2}$.
点评 本题考查直线和圆相交的性质,基本不等式的应用,解题的突破口是判断直线过圆心,解题的关键是利用a+b=1.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:选择题
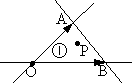 如图,已知O,A,B是平面内不共线的三点,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,直线OA,OB,AB将平面区域分成7部分,若点P落在区域①中(含边界),则z=2x+y的最大值为( )
如图,已知O,A,B是平面内不共线的三点,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,直线OA,OB,AB将平面区域分成7部分,若点P落在区域①中(含边界),则z=2x+y的最大值为( )| A. | 不存在 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-1)+f(-2)<2f(-$\frac{3}{2}$) | B. | f(-1)+f(-2)>2f(-$\frac{3}{2}$) | C. | f(-1)+f(-2)≤2f(-$\frac{3}{2}$) | D. | f(-1)+f(-2)≥2f(-$\frac{3}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 文科 | 理科 | |
| 数学优秀 | 10 | 13 |
| 数学不优秀 | 20 | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com