(Ⅰ)解:∵定义在R上的函数f(x)满足f(x+y)=f(x)•f(y)(x,y∈R),
且当x>0时,f(x)>1,f(2)=4,
∴f(2)=f(1+1)=f(1)•f(1)=4,
∴f(1)=2,或f(1)=-2(舍).
故f(1)=2.
∵f(1)=f((-1)+2)=f(-1)•f(2),
∴f(-1)=

=

=

.
(Ⅱ)证明:设x
1,x
2∈R且x
1<x
2,则f(x
2)-f(x
1)=f[(x
2-x
1)+x
1]-f(x
1)=f(x
1)[f(x
2-x
1)-1]
∵x
2-x
1>0,
∴f(x
2-x
1)>1
∴f(x
2-x
1)-1>0,
∵f(x
1)=f(

)=[f(
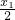
)]
2>0,
∴f(x
1)f[(x
2-x
1)-1]>0,
∴f(x
2)>f(x
1),
故f(x)在R上是增函数.
(III)解:∵

,
∴f(x
2-ax+a)•f(x
2-ax+a)=f(2x
2-2ax+2a)≥2=f(1),
∵f(x)在R上是增函数,
∴2x
2-2ax+2a≥1,
∴由

对任意x∈(1,+∞)恒成立,
得2x
2-2ax+2a≥1对任意x∈(1,+∞)恒成立,
∵y=2x
2-2ax+2a-1的对称轴是x=

,
∴在[

,+∞)上y=2x
2-2ax+2a-1是单调递增函数.
∵2x
2-2ax+2a≥1对任意x∈(1,+∞)恒成立,
∴

≤1,故a≤2.
∴实数a的取值范围(-∞,2].
分析:(Ⅰ)由题设条件知f(2)=f(1+1)=f(1)•f(1)=4,f(1)=f((-1)+2)=f(-1)•f(2),由此能求出f(1)和f(-1).
(Ⅱ)设x
1,x
2∈R且x
1<x
2,则f(x
2)-f(x
1)=f[(x
2-x
1)+x
1]-f(x
1)=f(x
1)[f(x
2-x
1)-1],由x
2-x
1>0,知f(x
2-x
1)-1>0,再由f(x
1)=f(

)=[f(
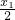
)]
2>0,能够证明f(x)在R上是增函数.
(III)由

,知f(x
2-ax+a)•f(x
2-ax+a)=f(2x
2-2ax+2a)≥2=f(1),再由f(x)在R上是增函数,能够求出实数a的取值范围.
点评:本题考查抽象函数的应用,考查函数的单调性的判断与证明,突出考查等价转化思想的运用,考查基本不等式,综合性强,难度大,属于难题.

 对任意x∈(1,+∞)恒成立,求实数a的取值范围.
对任意x∈(1,+∞)恒成立,求实数a的取值范围. =
= =
= .
. )=[f(
)=[f(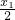 )]2>0,
)]2>0, ,
, 对任意x∈(1,+∞)恒成立,
对任意x∈(1,+∞)恒成立, ,
, ,+∞)上y=2x2-2ax+2a-1是单调递增函数.
,+∞)上y=2x2-2ax+2a-1是单调递增函数. ≤1,故a≤2.
≤1,故a≤2. )=[f(
)=[f(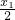 )]2>0,能够证明f(x)在R上是增函数.
)]2>0,能够证明f(x)在R上是增函数. ,知f(x2-ax+a)•f(x2-ax+a)=f(2x2-2ax+2a)≥2=f(1),再由f(x)在R上是增函数,能够求出实数a的取值范围.
,知f(x2-ax+a)•f(x2-ax+a)=f(2x2-2ax+2a)≥2=f(1),再由f(x)在R上是增函数,能够求出实数a的取值范围.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案