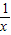练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    “x＞1”是“＜1”的（ ）条件．
    A．充分不必要
    B．必要不充分
    C．充要条件
    D．既不充分也不必要
    【答案】分析：求出分式不等式的解，利用充要条件的判断方法判断即可．
    解答：解：因为＜1的解为：x＜0或x＞1，所以“x＞1”是“＜1”的充分不必要条件．
    故选A．
    点评：本题考查分式不等式的解法，充要条件的判断方法．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    下列说法错误的是（　　）

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：013

    不等式(1+x)(1-|x|)>0的解集是（　）

    A．{x|0£x<1}　　　　　　　　　　　　　　　　　　　　　　    B．{x|x<0且x¹1}

    D．{x|-1<x<1}　　　　　　　　　　　　　　　　　　　　　　 D．{x|x<1且x¹-1}

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

    不等式(1+x)(1-|x|)>0的解集是（　）

    A．{x|0£x<1}　　　　　　　　　　　　　　　　　　　　　　    B．{x|x<0且x¹1}

    D．{x|-1<x<1}　　　　　　　　　　　　　　　　　　　　　　 D．{x|x<1且x¹-1}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    解：因为有负根，所以在y轴左侧有交点，因此

    解：因为函数没有零点，所以方程无根，则函数y=x+|x-c|与y=2没有交点，由图可知c>2


     13．证明：（1）令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0

    若f(1)=0，f(0)=f(1×0)=f(1)f(0)=0，所以f(1)=f(0)与已知条件“”矛盾所以f(1)≠0，因此f(1)=1,所以f(1)-1=0，1是函数y=f(x)-1的零点

    （2）因为f(1)=f[(-1)×（-1）]=f2(-1)=,所以f(-1)=±1，但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1，只能等于-1。所以任x∈R，f(-x)=f(-1)f(x)=-f(x)，因此函数是奇函数

    数字1，2，3，4恰好排成一排，如果数字i（i=1，2，3，4）恰好出现在第i个位置上则称有一个巧合，求巧合数的分布列。

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    下列说法错误的是


    1. A.
      命题：“已知f（x）是R上的增函数，若a+b≥0，则f（a）+f（b）≥f（-a）+f（-b）”的逆否命题为真命题
    2. B.
      “x＞1”是“|x|＞1”的充分不必要条件
    3. C.
      若p且q为假命题，则p、q均为假命题
    4. D.
      命题p：“?x∈R，使得x2+x+1＜0”，则　p：“?x∈R，均有x2+x+1≥0”

    查看答案和解析>>

    同步练习册答案