解:(1)∵数列{a
n}的前n项和为S
n,且S
n=n
2,
∴当n≥2时,a
n=S
n-S
n-1=n
2-(n-1)
2=2n-1.
当n=1时,a
1=S
1=1亦满足上式,
故a
n=2n-1,(n∈N*).
又数列{b
n}为等比数列,设公比为q,
∵b
1=1,b
4=b
1q
3=8,∴q=2.
∴b
n=2
n-1(n∈N*).
(2)

.
T
n=c
1+c
2+c
3+…c
n=(2
1-1)+(2
2-1)+…+(2
n-1)=(2
1+2
2+…2
n)-n=

.
所以 T
n=2
n+1-2-n.
(3)假设数列{c
n}中存在三项c
m,c
k,c
l成等差数列,不妨设m<k<l(m,k,l∈N*)
因为 c
n=2
n-1,
所以 c
m<c
k<c
l,且三者成等差数列.
所以 2c
k=c
l+c
m,
即2(2
k-1)=(2
m-1)+(2
l-1),
变形可得:2•2
k=2
m+2
l=2
m(1+2
l-m)
所以

,即2
k+1-m=1+2
l-m.
所以 2
k+1-m-2
l-m=1.
因为m<k<l(m,k,l∈N*),
所以 2
k+1-m,2
l-m均为偶数,而1为奇数,
所以等式不成立.
所以数列{c
n}中不存在三项,使得这三项成等差数列.
分析:(1)对于数列{a
n},已知S
n=n
2,利用递推公式可求当n≥2时,a
n=S
n-S
n-1,当n=1时,a
1=S
1=1可求a
n,对于数列{b
n},是等比数列,设公比为q,及b
1=1,b
4=b
1q
3=8,可求q,进而可求b
n(2)由题意可得,
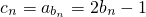
=2
n-1,结合数列的特点可考虑利用分组求和,结合等差数列及等比数列的求和公式可求;
(3)假设数列{c
n}中存在三项c
m,c
k,c
l成等差数列,则2c
k=c
l+c
m,由(2)可得2(2
k-1)=(2
m-1)+(2
l-1),变形可得2•2
k=2
m+2
l=2
m(1+2
l-m),进而可变形为2
k+1-m-2
l-m=1,由整数的性质可得矛盾,即可以得打结论.
点评:本题综合考查等比数列、与等差数列,涉及数列的等差、等比的性质、等差数列的判定以及数列的求和,需要全面掌握数列的有关性质.

 ,求数列{cn}的前n项和Tn;
,求数列{cn}的前n项和Tn; .
. .
. ,即2k+1-m=1+2l-m.
,即2k+1-m=1+2l-m.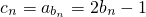 =2n-1,结合数列的特点可考虑利用分组求和,结合等差数列及等比数列的求和公式可求;
=2n-1,结合数列的特点可考虑利用分组求和,结合等差数列及等比数列的求和公式可求;

 阅读快车系列答案
阅读快车系列答案