Question

19．空气污染，又称为大气污染，当空气污染指数（单位：μg/m³）为0～50时，空气质量级别为一级，空气质量
状况属于优；当空气污染指数为50～100时，空气质量级别为二级，空气质量状况属于良；当空气污染指数为
100～150时，空气质量级别为三级，空气质量状况属于轻度污染；当空气污染指数为150～200时，空气质量级别为四级，空气质量状况属于中度污染； 2015年1月某日某省x个监测0点数据统计如下：

空气污染指数 （单位：μg/m3）	[0，50]	（50，100]	（100，150]	（150，200]
监测点个数	15	40	y	15

（Ⅰ）根据所给统计表和频率分布直方图中的信息求出x，y的值，并完成频率分布直方图；
（Ⅱ）统计部门从该省空气质量“良好”和“轻度污染”的两类监测点中采用分层抽样的方式抽取了7个监测点，省环保部门再从中随机选取3个监测点进行调研，记省环保部门“选到空气质量“良好”的城市个数为ξ”，求ξ的分布列．

Answer 1

分析 （Ⅰ）由题意得0.003×50=$\frac{15}{x}$，15+40+y+15=x，由此能求出x，y，进而能完成频率分布直方图．
（Ⅱ）空气良好有$\frac{7}{40+30}×40=4$个，轻度污染有$\frac{7}{40+30}×30=3$个，ξ的所有可能取值为0，1，2，3，分别求出相应的概率，由此能求出ξ的分布列．

解答 解：（Ⅰ）由题意得0.003×50=$\frac{15}{x}$，解得x=100，
又15+40+y+15=100，解得y=30．
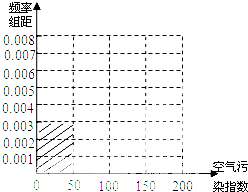
∵$\frac{40}{100×50}$=0.008，$\frac{30}{100×50}=0.006$，$\frac{15}{100×50}=0.003$，
∴完成频率分布直方图，如下图：

（Ⅱ）空气良好有$\frac{7}{40+30}×40=4$个，轻度污染有$\frac{7}{40+30}×30=3$个，
ξ的所有可能取值为0，1，2，3，
P（ξ=0）=$\frac{{C}_{3}^{3}}{{C}_{7}^{3}}$=$\frac{1}{35}$，
P（ξ=1）=$\frac{{C}_{4}^{1}{C}_{3}^{2}}{{C}_{7}^{3}}$=$\frac{12}{35}$，
P（ξ=2）=$\frac{{C}_{4}^{2}{C}_{3}^{1}}{{C}_{7}^{3}}$=$\frac{18}{35}$，
P（ξ=3）=$\frac{{C}_{4}^{3}{C}_{3}^{0}}{{C}_{7}^{3}}$=$\frac{4}{35}$，
∴ξ的分布列为：

ξ	0	1	2	3
P	$\frac{1}{35}$	$\frac{12}{35}$	$\frac{18}{35}$	$\frac{4}{35}$

点评 本题考查频率分布直方图的应用，考查离散型随机变量的分布列的求法，是基础题，解题时要认真审题，注意排列组合知识的合理运用．