
已知a>0,b∈R,函数f(x)=4ax3-2bx-a+b.
(Ⅰ)证明:当0≤x≤1时,
(ⅰ)函数f(x)的最大值为|2a-b|﹢a;
(ⅱ)f(x)+|2a-b|﹢a≥0;
(Ⅱ)若-1≤f(x)≤1对x∈[0,1]恒成立,求a+b的取值范围.
|
答案:(Ⅰ)见解析;(Ⅱ) 解析:本题主要考察不等式,导数,单调性,线性规划等知识点及综合运用能力. (Ⅰ)(ⅰ) 当b≤0时, 此时 当b>0时, 此时 综上所述:函数 (ⅱ)要证 亦即证 ∵ 当b≤0时, 此时 当b<0时, ≤|2a-b|﹢a; 综上所述:函数 即 (Ⅱ)由(Ⅰ)知:函数 且函数 ∵-1≤ ∴|2a-b|﹢a≤1. 取b为纵轴,a为横轴. 则可行域为: 作图如下:
由图易得:当目标函数为z=a+b过P(1,2)时,有 ∴所求a+b的取值范围为: |


科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:浙江省高考真题 题型:解答题
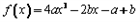 。
。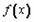 的最大值为|2a-b|﹢a;
的最大值为|2a-b|﹢a; +|2a-b|﹢a≥0;
+|2a-b|﹢a≥0;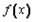 ≤1对x∈[0,1]恒成立,求a+b的取值范围。
≤1对x∈[0,1]恒成立,求a+b的取值范围。查看答案和解析>>
科目:高中数学 来源:2012年浙江省高考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com