
.己知数列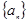 满足
满足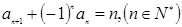 ,则数列
,则数列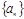 的前2016项的和
的前2016项的和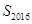 的值是___________.
的值是___________.
1017072
【解析】
试题分析:这个数列既不是等差数列也不是等比数列,因此我们要研究数列的各项之间有什么关系,与它们的和有什么联系?把已知条件具体化,有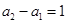 ,
,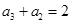 ,
,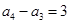 ,
,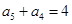 ,…,
,…,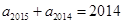 ,
,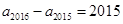 ,我们的目的是求
,我们的目的是求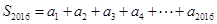 ,因此我们从上面2015个等式中寻找各项的和,可能首先想到把出现“+”的式子相加(即
,因此我们从上面2015个等式中寻找各项的和,可能首先想到把出现“+”的式子相加(即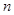 为偶数的式子相加),将会得到
为偶数的式子相加),将会得到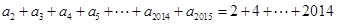 ,好像离目标很近了,但少
,好像离目标很近了,但少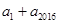 ,而
,而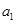 与
与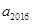 分布在首尾两个式子中,那么能否把首尾两个式子相减呢?相减后得到
分布在首尾两个式子中,那么能否把首尾两个式子相减呢?相减后得到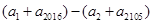
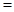
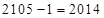 ,为了求
,为了求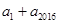 ,我们又不得不求
,我们又不得不求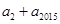 ,依次下去,发现此路可能较复杂或者就行不通,重新寻找思路,从头开始我们有
,依次下去,发现此路可能较复杂或者就行不通,重新寻找思路,从头开始我们有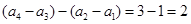 ,即
,即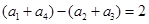 ,而
,而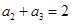 ,∴
,∴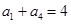 ,因此
,因此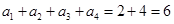 ,我们由开始的三个等式求出了
,我们由开始的三个等式求出了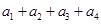 ,是不是还可用这种方法求出
,是不是还可用这种方法求出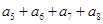 呢?下面舍去
呢?下面舍去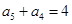 ,考察
,考察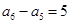 ,
,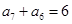 ,
,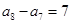 ,同样方法处理,
,同样方法处理,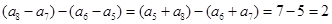 ,从而
,从而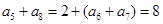 ,于是
,于是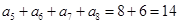 ,而
,而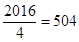 ,正好504组,看来此法可行,由此我们可得
,正好504组,看来此法可行,由此我们可得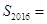
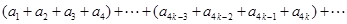
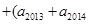
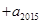
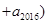
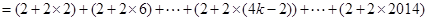
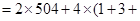
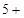

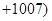
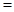
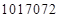 .
.
考点:分组求和.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013-2014学年北京市石景山区高三年级第一学期期末文科数学试卷(解析版) 题型:解答题
已知集合 ,对于数列
,对于数列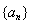 中
中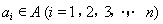 .
.
(Ⅰ)若三项数列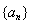 满足
满足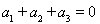 ,则这样的数列
,则这样的数列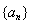 有多少个?
有多少个?
(Ⅱ)若各项非零数列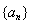 和新数列
和新数列 满足首项
满足首项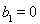 ,
,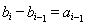 (
(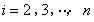 ),且末项
),且末项 ,记数列
,记数列 的前
的前 项和为
项和为 ,求
,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海黄浦区高三上学期期末考试(即一模)文数学卷(解析版) 题型:填空题
.己知数列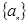 满足
满足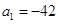 ,
,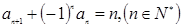 ,则数列
,则数列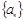 的前2013项的和
的前2013项的和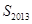 的值是___________.
的值是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com