
分析 (1)利用导数的几何意义,求a的值;
(2)当-1<a<0时,求导数,确定函数的单调性,即可求函数f(x)的极值点.
解答 解:(1)$f'(x)=x+a-1-\frac{a}{x}$…(2分)
∵f'(2)=-1,∴$2+a-1-\frac{a}{2}=-1$,∴a=-4…(2分)
(2)由(1)知,$f'(x)=x+a-1-\frac{a}{x}=\frac{{{x^2}+(a-1)x-a}}{x}=\frac{(x+a)•(x-1)}{x}$…(1分)
定义域为(0,+∞)∵-1<a<0,∴0<-a<1…(1分)
令f'(x)=0则 x=-a或x=1…(1分)
| x | (0,-a) | -a | (-a,1) | 1 | (1,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↑ | 极大值 | ↓ | 极小值 | ↑ |
点评 本题考查导数知识的综合运用,考查导数的几何意义的运用,考查函数的极值,考查函数的单调性问题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
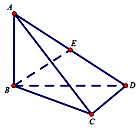 如图:在空间四边形ABCD中,已知AB⊥BC,AB⊥BD,BC⊥CD且AB=BC=6,BD=8,E为AD中点,求异面直线BE与CD所成角.
如图:在空间四边形ABCD中,已知AB⊥BC,AB⊥BD,BC⊥CD且AB=BC=6,BD=8,E为AD中点,求异面直线BE与CD所成角.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
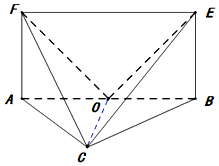 如图,四边形ABEF为矩形,AC=BC,AB=2AF=FC=2,$OC=\sqrt{2}$.O为AB的中点.
如图,四边形ABEF为矩形,AC=BC,AB=2AF=FC=2,$OC=\sqrt{2}$.O为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
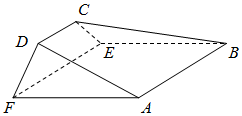 如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为矩形,AF⊥DF,且二面角D-AF-E与二面角C-BE-F都等于$α(0<α<\frac{π}{2})$.
如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为矩形,AF⊥DF,且二面角D-AF-E与二面角C-BE-F都等于$α(0<α<\frac{π}{2})$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
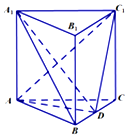 如图,直三棱柱ABC-A1B1C1中,△ABC是等边三角形,D是BC的中点.
如图,直三棱柱ABC-A1B1C1中,△ABC是等边三角形,D是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (1,+∞) | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com